- 7 maja 2024
- Posted by: Maurycy Gast
- Category: Nauka przyjemna i skuteczna

Jedną z podstawowych definicji, z którą należy się zapoznać, ucząc się programowania, jest rekurencja. Przydaje się ona przy tworzeniu kodu, o czym przekonało się już wielu programistów. Jej znajomość jest też wymagana na maturze z informatyki.
Co to jest rekurencja w informatyce?
Rekurencja (rekursja) to odwołanie się funkcji do samej siebie w trakcie działania programu. Wystarczy nawet pojedyncze wywołanie się procedury przez samą siebie, żeby uznać ją za rekurencyjną.

1 2 3 4 | funkcja Silnia (n) jeżeli n = 0 lub n = 1 wykonuj zwróć 1 zwróć n * Silnia(n - 1) |
Wykonanie powyższego kodu wygląda następująco dla n = 3 (każde wcięcie to kolejny poziom wywołania rekurencyjnego):
- Silnia(3) – Warunek nie jest spełniony, bo n = 3, więc przechodzimy do mnożenia: 3 * Silnia(2).
- Silnia(2) – Warunek nie jest spełniony, bo n = 2, więc przechodzimy do mnożenia: 2 * Silnia(1).
- Silnia(1) – Warunek jest spełniony, bo n = 1, więc zwracamy 1.
- Powrót do Silnia(2) (kontynuacja) – Mnożymy wynik z Silnia(1) (czyli 1) przez 2, więc wynikiem jest 2.
- Powrót do Silnia(3) (kontynuacja) – Mnożymy wynik z Silnia(2) (czyli 2) przez 3, więc wynikiem jest 6.
Powyższy przykład to zastosowanie rekurencji w ramach obliczania silni, co pozwala znacznie uprościć napisany kod.

Podział rekurencji według sposobu wywołania:
- Rekurencja pośrednia – funkcja jest wywoływana przez inną funkcję, wywołaną (pośrednio lub bezpośrednio) przez samą funkcję (np. funkcja A wywołuje B, funkcja B wywołuje A…),
- Rekurencja bezpośrednia – funkcja wywołuje samą siebie bezpośrednio wewnątrz ciała funkcji (rozwiązanie spotykane częściej – funkcja F wywołuje funkcję F…).
Podział rekurencji według wzrostu liczby wywołań:
- Rekurencja liniowa (single recursion) – chodzi o liniowy wzrost wywołań rekurencji, co jest zależne od wielkości danych wejściowych. Następuje tylko jedno wywołanie w czasie pojedynczego wykonywania funkcji (np. funkcja A wywołuje funkcję A, która następnie znowu wywołuje funkcję A).
- Rekurencja nieliniowa (multiple recursion) – w czasie pojedynczego wywołania następuje większa liczba kolejnych wywołań. Ogólna liczba wywołań nie jest tak zależna od wielkości danych wejściowych, rośnie więc znacznie szybciej (np. funkcja A wywołuje funkcję A w dwóch miejscach). Ze względu na większe skomplikowanie mogą tu nastąpić problemy z wydajnością, a także zużyciem pamięci.
Rekurencja ogonowa następuje wtedy, kiedy ostatnią instrukcją danej funkcji jest jej kolejne wywołanie. Pozwala to na optymalizację kodu, bo program nie utrzymuje zapisanych danych w stosie z każdego wywołania funkcji. Zamiast tego przekazuje argument (lub kilka) bez zapisu dodatkowych danych. Dodatkowo taki sposób zapisu procedury umożliwia łatwą jej konwersję na iterację, a więc możesz bez problemu zamienić rekurencję na pętlę.
Do najpopularniejszych algorytmów korzystających z rekurencji należy ciąg Fibonacciego. Dla przypomnienia – jest to ciąg liczb naturalnych, w którym każda liczba jest sumą dwóch poprzednich (za wyjątkiem pierwszej i drugiej z uwagi na brak dwóch wartości poprzedzających). Zastosowanie tego ciągu jest niezwykle szerokie – stosują go nawet inwestorzy giełdowi w celu określenia prawdopodobieństwa wzrostów i spadków. Warto zauważyć, że ten ciąg zaczyna się zazwyczaj od n = 0 lub n = 1, ale jako że ciągi są oparte o liczby naturalne n > 0, w poniższym przypadku funkcji oraz drzewa rozpoczynamy od n = 1.
Przedstawienie tego ciągu w sposób iteracyjny wyglądałoby następująco:
1 2 3 4 5 6 7 8 9 10 | funkcja fib(n) przedwcześniej ← 0 wcześniej ← 0 teraz ← 1 dla i = 1, 2, … n - 1 wykonuj przedwcześniej ← wcześniej wcześniej ← teraz teraz ← przedwcześniej + wcześniej zwróć teraz |
Z kolei rekurencyjny zapis ciągu Fibonacciego prezentowałby się tak:
1 2 3 4 5 6 | funkcja fib(n) jeżeli n = 1 wykonuj zwróć 1 jeżeli n = 2 wykonuj zwróć 1 zwróć fib(n-1) + fib(n-2) |

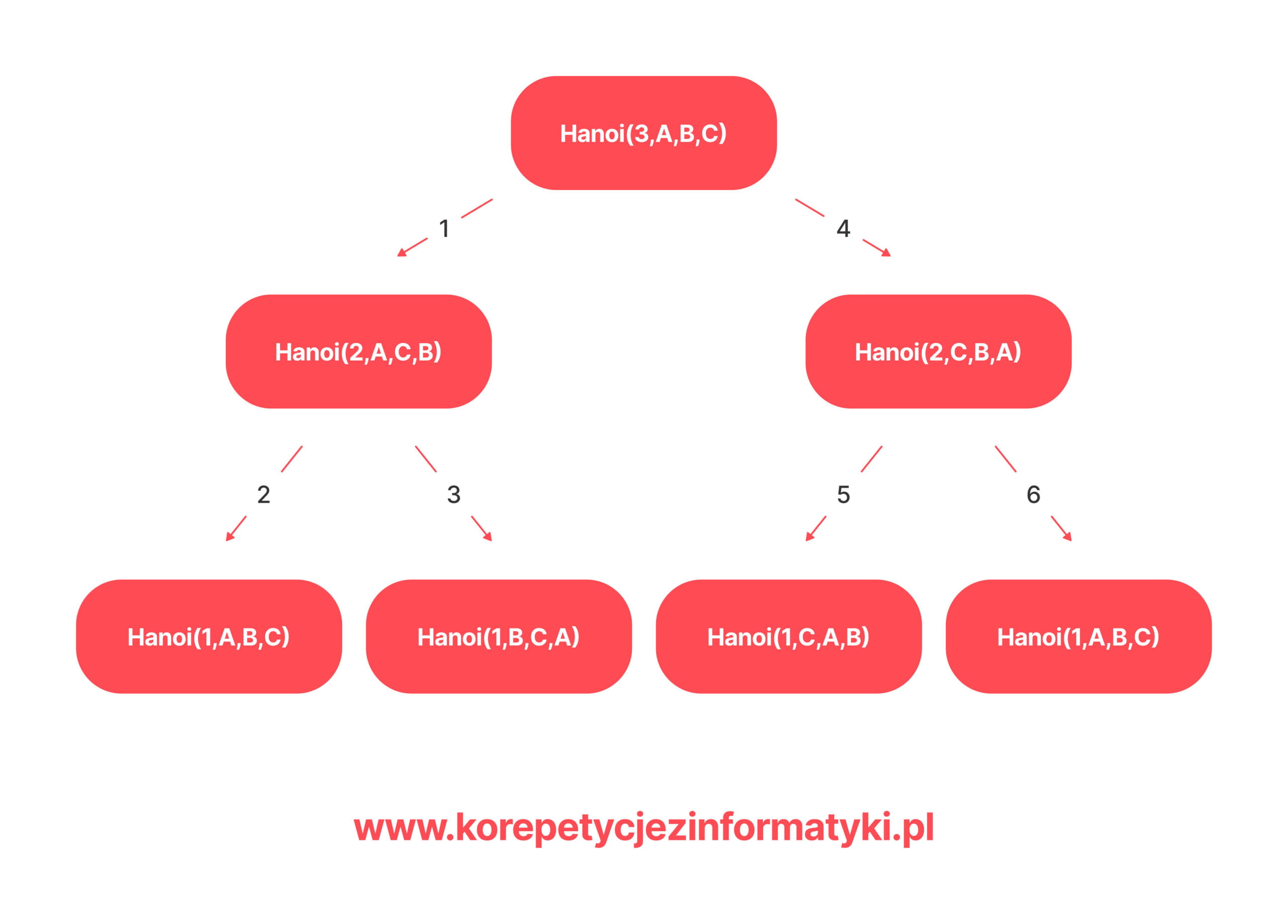
Drzewo wywołań rekurencyjnych to struktura graficzna przedstawiająca kolejne wywołania rekurencyjne danej funkcji. Powyżej znajdziesz jej przykład na bazie ciągu Fibonacciego. Każdy węzeł w drzewie reprezentuje jedno wywołanie rekurencyjne, a gałęzie wychodzące z węzłów to kolejne wywołania z wnętrza danej funkcji. Korzeń drzewa obrazuje początkowe wywołanie funkcji, a liście są końcowymi przypadkami rekurencji, w których funkcja przestaje się wywoływać.
Drzewo wywołań rekurencyjnych pozwala wizualizować kolejność i strukturę wywołań rekurencyjnych, co może być przydatne do analizy działania funkcji rekurencyjnej, identyfikacji przypadków bazowych oraz zrozumienia złożoności algorytmu rekurencyjnego.
Co ciekawe, kwestią sporną i umowną jest włączanie zera jako pierwszego elementu ciągu Fibonacciego. Jednak w zadaniach maturalnych należy traktować 0 jako liczbę naturalną, jeśli nie jest inaczej powiedziane.
Rekurencja – zalety i wady
Większość osób nie jest zaznajomiona z zaletami oraz wadami rekurencji. Warto zapoznać się z nimi, dla zrozumienia czemu jest to nadal wykorzystywany sposób działania w przypadku rozmaitych programów.
Jakie są zalety rekurencji?
- Zwięzły i czytelny kod – w przypadku określonych algorytmów rekurencja prowadzi do znacznego uproszczenia kodu (przykładowo jeśli chodzi o silnię),
- Możliwość udowodnienia poprawności (indukcja matematyczna) – przy różnych rozwiązaniach rekurencyjnych z pomocą indukcji matematycznej można udowodnić, że algorytm działa poprawnie dla wszystkich rozmiarów problemu,
- Caching (memoizacja) – możliwość optymalizacji algorytmu rekurencyjnego dzięki zapisowi wyników, które regularnie się powtarzają (argumenty są identyczne), co zmniejsza liczbę wykonywanych obliczeń,
- Brak modyfikacji globalnej pamięci – można doprowadzić do sytuacji, w której funkcja operuje tylko na kilku „własnych” zmiennych.
Jakie są wady rekurencji?
- Jest pamięciochłonna – w wielu przypadkach użycie rekurencji może prowadzić do nadmiernego wykorzystywania stosu (pamięci – przykładowo jeśli chodzi o sortowanie przez scalanie), co ma wpływ m.in. na szybkość działania programu (jest to widoczne przy dużych obliczeniach),
- Jest mniej intuicyjna – należy nabrać pewnej wprawy, żeby skutecznie, bez popełniania błędów korzystać z rekurencji w czasie kodowania.
Okazuje się, że w informatyce zastosowanie rekurencji nie zawsze jest efektywne. Wręcz przeciwnie, pytani o rekurencję, informatycy często odpowiadają: „unikamy, kiedy się da”. Każdorazowo zwiększa ona zapotrzebowanie programu na pamięć, ponieważ każde kolejne wywołanie funkcji wymaga zapamiętania pewnych informacji, które są niezbędne do odtworzenia stanu sprzed wywołania (rekurencja ogonowa ogranicza skalę tego problemu). Jeżeli funkcje muszą wykonać się zbyt wiele razy, komputer może napotkać spore problemy podczas ich obliczania. Świetnym przykładem może być tutaj obliczanie silni dla 1000 lub też liczenie setnego elementu wspomnianego już ciągu Fibonacciego. Warto też spojrzeć na drzewo wywołań rekurencyjnych podane wcześniej, gdzie kilkukrotnie wywoływana jest funkcja o tym samym argumencie, a więc te same wartości liczy się kilka razy.
Stosując rekursję, musisz być także ostrożny w definiowaniu warunku brzegowego. Jeżeli zdefiniujesz go niewłaściwie, możesz spowodować, że funkcja będzie się wywoływać w nieskończoność, a więc wykonanie elementarne nie nastąpi.
Kiedy używać rekurencji, a kiedy iteracji?
Często problematyczne okazuje się zrozumienie, kiedy używać rekurencji, a kiedy iteracji (pętli). Poniżej znajdziesz sytuacje, kiedy warto zdecydować się na zastosowanie konkretnej metody, biorąc pod uwagę zalety jakie posiadają.
- Problem ma rekurencyjną naturę – część rozwiązań danego zagadnienia jest stworzona typowo pod rekurencję,
- Struktura danych jest rekurencyjna – przykładowo chodzi o takie struktury jak grafy lub drzewa,
- Możliwy jest podział na podobne podproblemy – jeśli dany problem możesz łatwo podzielić na mniejsze podproblemy, które są praktycznie takie same, to rekurencja okazuje się idealnym rozwiązaniem.
- Problem jest prosty – pętle pozwolą napisać kod przy najmniejszym wymaganym nakładzie czasu,
- Potrzebna jest dokładna kontrola nad pamięcią – iteracja umożliwia łatwą kontrolę nad danymi, więc pozwoli szybko ograniczyć ilość zużywanej pamięci,
- Prostota kodu jest istotna – jeśli kod będzie czytany przez inne osoby, a rekurencja nie jest wymagana, to dobrze zdecydować się na iterację.
Przykłady algorytmów rekurencyjnych – gdzie stosuje się rekurencję?
Rekurencja w informatyce, podobnie jak w matematyce, jest często stosowana. Można ją znaleźć w takich rozwiązaniach jak:
- Silnia (Factorial),
- Ciąg Fibonacciego (Fibonacci Sequence),
- Suma elementów listy (Sum of List Elements),
- Wyszukiwanie binarne (Binary Search),
- Dzielenie całkowite z odejmowaniem (Integer Division with Subtraction),
- Szybkie potęgowanie (Fast Exponentiation),
- Sortowanie przez scalanie (Merge Sort),
- Sortowanie szybkie (QuickSort),
- Drzewo Binomialne (Binomial Tree),
- Wieże Hanoi (Tower of Hanoi),
- Algorytmy grafowe DFS/BFS (Graph Algorithms – DFS/BFS),
- Algorytm podziału zbioru (Subset Sum),
- Algorytm najdłuższego wspólnego podciągu (Longest Common Subsequence),
- Algorytm programowania dynamicznego (Dynamic Programming),
- Algorytmy drzewiaste AVL/Red-Black (AVL Tree/Red-Black Tree Algorithms),
- Algorytm rozwiązywania labiryntów (Maze Solving).
Zastosowanie rekurencji – przykład implementacji algorytmu Wieże Hanoi
Wieże Hanoi to klasyczny problem rekurencyjny, sformułowany przez Édouarda Lucasa w 1883 roku. Zadanie polega na przeniesieniu stosu krążków z jednej kolumny na inną przy zachowaniu kilku zasad:
- Krążki są ułożone w stosie w malejącej kolejności (pod względem średnicy), tzn. największy jest na dole, a najmniejszy na górze,
- Tylko jeden krążek może zostać przeniesiony w danym czasie,
- Krążki można przenosić tylko na pusty słupek lub na ten, na którym znajduje się krążek większy od tego, który ma być przeniesiony,
Celem jest przeniesienie wszystkich krążków z jednego stosu na drugi, przy użyciu trzeciego jako pomocniczego, z minimalną liczbą ruchów.
Objaśnienie zmiennych:
- pkolumna – nazwa kolumny początkowej,
- dkolumna – nazwa kolumny docelowej,
- gkolumna – nazwa kolumny pomocniczej,
- n – liczba krążków.
Wieże Hanoi – rekurencja: schemat blokowy i pseudokod
Wieże Hanoi to algorytm niezwykle często podawany w szkole średniej, jako przykład działania rekurencji. Pozwala skutecznie zrozumieć na czym polega funkcja “wywołująca samą siebie”. Zapoznaj się z opisem działania pseudokodu, a także drzewem wywołań, okażą się pomocne w czasie nauki.
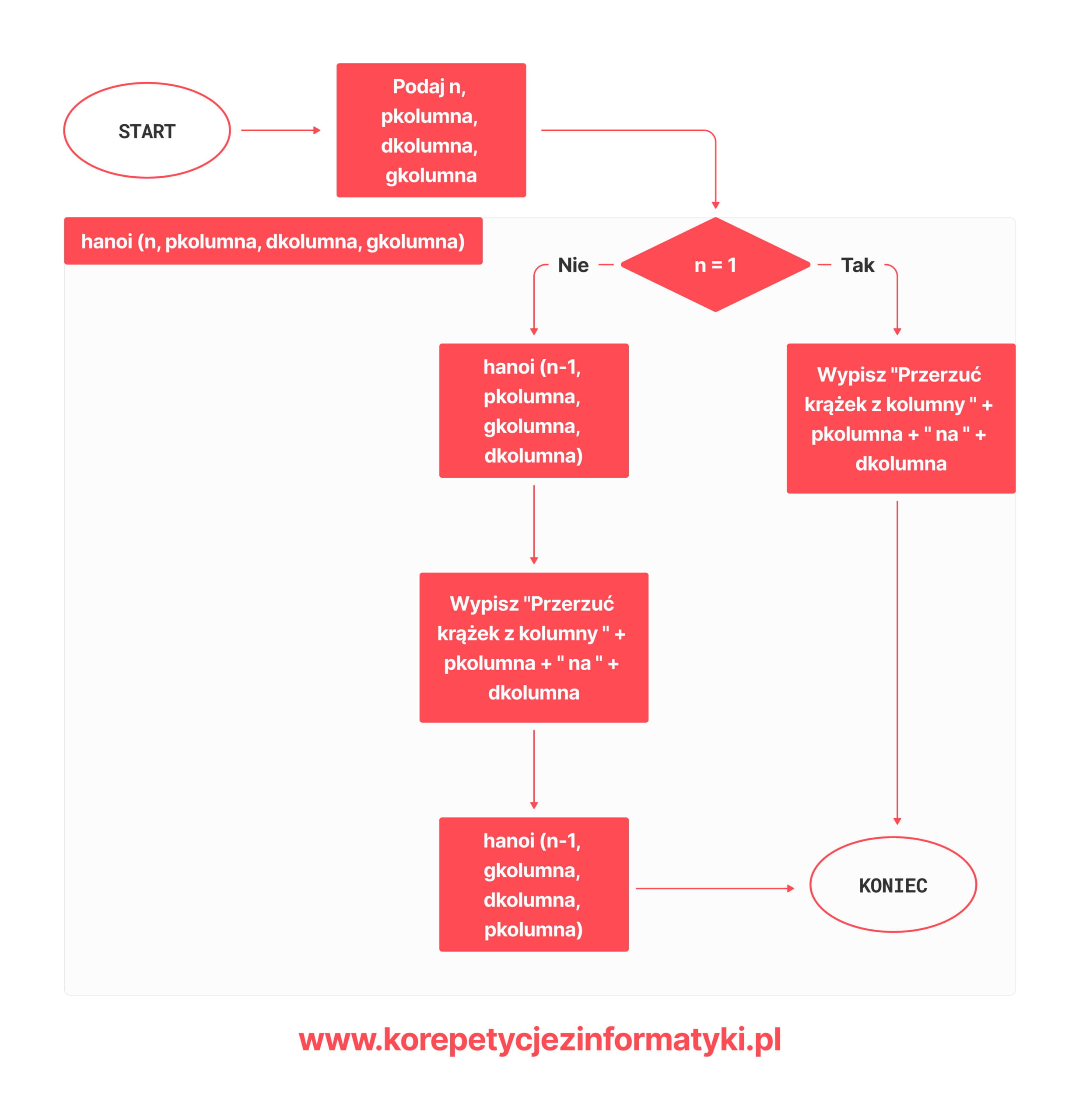
1 2 3 4 5 6 7 | funkcja hanoi (n, pkolumna, dkolumna, gkolumna) jeżeli n = 1 wykonuj wypisz ("Przerzuc krazek z kolumny " + pkolumna + " na " + dkolumna) w przeciwnym razie hanoi (n-1, pkolumna, gkolumna, dkolumna) wypisz ("Przerzuc krazek z kolumny " + pkolumna + " na " + dkolumna) hanoi (n-1, gkolumna, dkolumna, pkolumna) |
Opis rekurencyjnego algorytmu Wieże Hanoi – pseudokod
- 1 linia – definicja funkcji Hanoi, która przenosi krążki z jednej kolumny (pkolumna) na drugą (dkolumna) z pomocą dodatkowej (gkolumna),
- 2 linia – warunek elementarny: Jeśli jest tylko jeden krążek, przenieś go bez rekurencji (w tym przypadku po prostu wypisując ten proces),
- 4-5 linia – w przeciwnym razie wykonaj algorytm Hanoi dla n-1 krążków,
- 6 linia – przenieś największy krążek z kolumny źródłowej na kolumnę docelową,
- 7 linia – wywołaj funkcję hanoi (wywołanie funkcji w funkcji, a więc rekurencja) dla n-1 krążków na kolumnie pomocniczej jako kolumnie źródłowej.
Przykład zastosowania algorytmu Wieże Hanoi dla 3 krążków
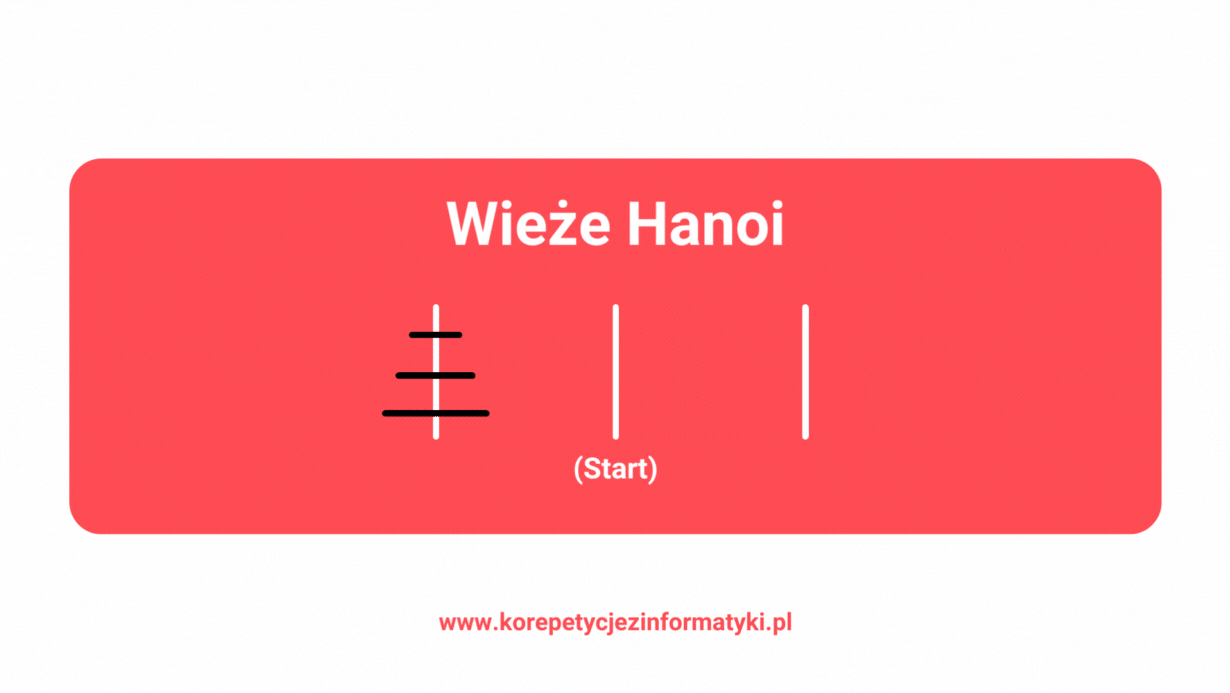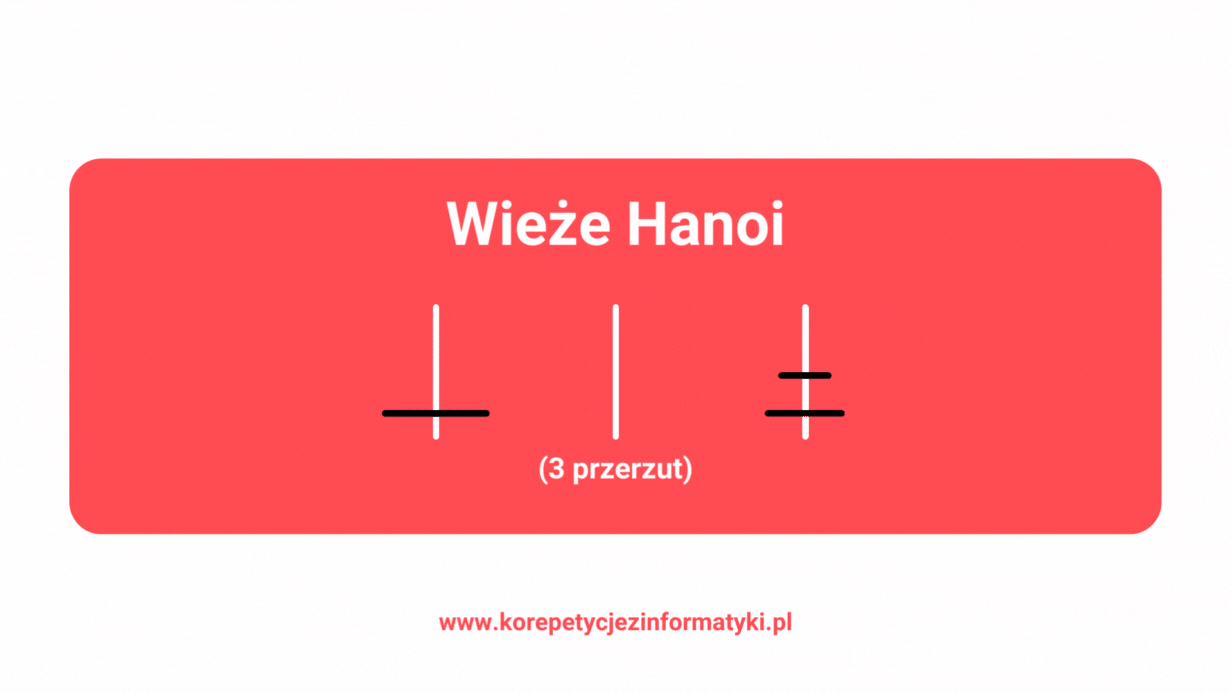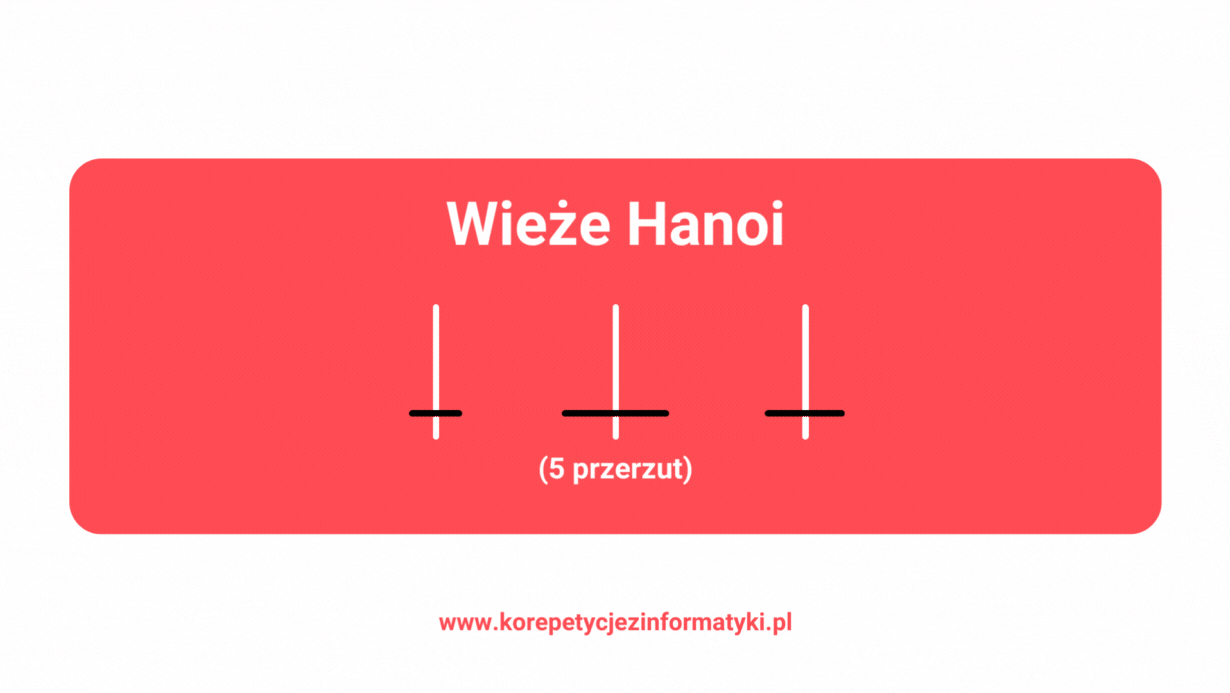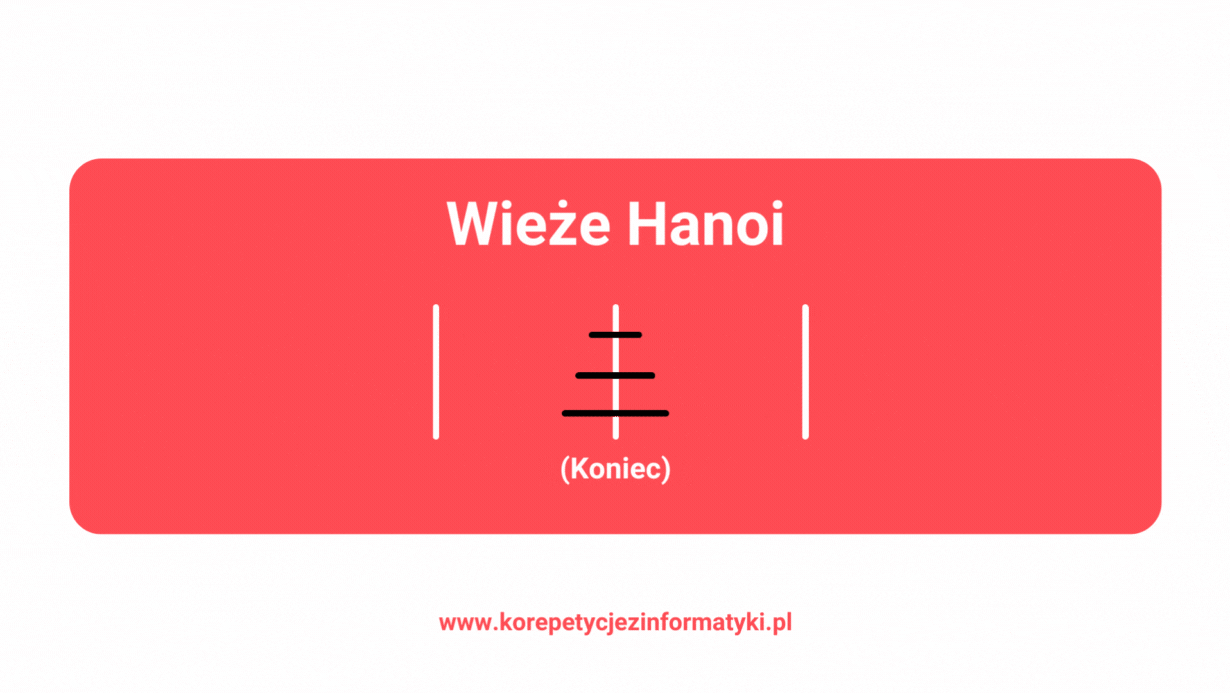
Poniżej znajdziesz wykonanie algorytmu Wież Hanoi krok po kroku, wywołanie po wywołaniu. Zapoznanie się z tym przykładem ułatwi Ci zrozumienie działania algorytmu. Zwróć uwagę na wcięcia, które wskazują kolejność wywołań rekurencyjnych, a także na końcowy nawias, gdzie opisano, która linia pseudokodu jest wykonywana.
- Hanoi(3,A,B,C) – główne wywołanie funkcji (1 linia).
- Hanoi(2,A,C,B) – wywołanie rekurencyjne (5 linia).
- Hanoi(1,A,B,C) – wywołanie rekurencyjne (5 linia).
- Z kolumny A na kolumnę B – przerzucenie krążka (3 linia).
- Z kolumny A na kolumnę C – przerzucenie krążka (6 linia).
- Hanoi(1,B,C,A) – wywołanie rekurencyjne (7 linia).
- Z kolumny B na kolumnę C – przerzucenie krążka (3 linia).
- Z kolumny A na kolumnę B – przerzucenie krążka (6 linia).
- Hanoi(2,C,B,A) – wywołanie rekurencyjne (7 linia).
- Hanoi(1,C,A,B) – wywołanie rekurencyjne (5 linia).
- Z kolumny C na kolumnę A – przerzucenie krążka (3 linia).
- Z kolumny C na kolumnę B – przerzucenie krążka (6 linia).
- Hanoi(1,A,B,C) – wywołanie rekurencyjne (7 linia).
- Z kolumny A na kolumnę B – przerzucenie krążka (3 linia).
Wieże Hanoi – rekurencja: Python, C++ i Java
Python – Wieże Hanoi
1 2 3 4 5 6 7 8 | def wHanoi(n, pkolumna, dkolumna, gkolumna): if n == 1: print(f"Przerzuc krazek z kolumny {pkolumna} na {dkolumna}") else: wHanoi(n-1, pkolumna, gkolumna, dkolumna) print(f"Przerzuc krazek z kolumny {pkolumna} na {dkolumna}") wHanoi(n-1, gkolumna, dkolumna, pkolumna) wHanoi(3, 'A', 'B', 'C') |
C++ – Wieże Hanoi
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | #include <iostream> using namespace std; void wHanoi(int n, char pkolumna, char dkolumna, char gkolumna) { if (n == 1) { cout << "Przerzuc krazek z kolumny " << pkolumna << " na kolumne " << dkolumna << endl; } else { wHanoi(n-1, pkolumna, gkolumna, dkolumna); cout << "Przerzuc krazek z kolumny " << pkolumna << " na kolumne " << dkolumna << endl; wHanoi(n-1, gkolumna, dkolumna, pkolumna); } } int main(){ wHanoi(3, 'A', 'B', 'C'); } |
Java – Wieże Hanoi
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | public class Main { public static void main(String[] args) { wHanoi(3, 'A', 'B', 'C'); } public static void wHanoi(int n, char pkolumna, char dkolumna, char gkolumna) { if (n == 1) { System.out.println("Przerzuc krazek z kolumny " + pkolumna + " na kolumne " + dkolumna); } else { wHanoi(n-1, pkolumna, gkolumna, dkolumna); System.out.println("Przerzuc krazek z kolumny " + pkolumna + " na kolumne " + dkolumna); wHanoi(n-1, gkolumna, dkolumna, pkolumna); } } } |
Rekurencja jest techniką użyteczną w przypadku części problemów (których struktura sprawia, że to naturalne rozwiązanie), a przy tym zajmuje niewiele miejsca, jeśli chodzi o kod. Jednak przy złych warunkach brzegowych można łatwo stworzyć błędy (nie nastąpi wykonanie elementarne, czyli zwrócenie wyniku) i mieć problemy z czasem działania programu, przez co jest to metoda zazwyczaj odradzana przez fachowców. Warto jednak dobrze zapoznać się z charakterystyką rekurencji i jej słabymi stronami. Jeśli dobrze ją opanujesz, może pomóc Ci w Twoich przyszłych programistycznych zmaganiach.
Najczęściej zadawane pytania o rekurencję w informatyce
Kiedy rekurencja sprawia problemy?
- Przepełnienie stosu – gdy problem jest złożony, a więc rekurencja musi zostać wywołana wiele razy, może to doprowadzić do osiągnięcia maksymalnej głębokości stosu (stack overflow). Jest to typowy błąd, przez który program nie jest w stanie prawidłowo działać.
- Problemy z wydajnością – choć zazwyczaj rozsądniejszym rozwiązaniem wydaje się zastosowanie pętli niż rekurencji, to w niektórych sytuacjach lepszym wyborem okazuje się jednak rekurencja, bo ze względu na złożoność problemu zastosowanie tej techniki okazuje się bardziej naturalne (także pod względem wydajności). Rekurencja pozwala na krótki zapis kodu, jednak problematyczne może okazać się duże zapotrzebowanie na pamięć i czas.
Jak zoptymalizować algorytmy rekurencyjne?
Caching (memoizacja) – to prosta, ale użyteczna technika, która polega na zapamiętaniu wyników wcześniejszych wywołań danej funkcji rekurencyjnej, dzięki czemu ogranicza się liczbę jej kolejnych powtórzeń (te same obliczenia nie są wykonywane drugi, trzeci czy kolejny raz).
Co to jest metoda rekurencyjna?
Metoda rekurencyjna to inna nazwa funkcji rekurencyjnej, a więc procedury, która wywołuje samą siebie w trakcie wykonywania.
Czym różni się rekurencja od iteracji?
- Rekurencja – w rekurencji funkcja rozkłada problem na mniejsze części, a następnie rozwiązuje każdą z nich przez wywołanie samej siebie. Wyniki podproblemów są łączone, aby uzyskać wynik dla całego problemu.
- Iteracja – w iteracji problem jest rozwiązywany za pomocą pętli, gdzie kolejne iteracje modyfikują aktualny stan aż do osiągnięcia końcowego wyniku. W przeciwieństwie do rekurencji iteracja nie polega na wywoływaniu samej siebie, ale na powtarzalnym wykonywaniu instrukcji.
Który algorytm jest rekurencyjny?
W przypadku gotowego rozwiązania łatwo rozpoznasz algorytm rekurencyjny, znajdując w nim wywołanie samego siebie. Natomiast w skończonym kodzie wystarczy wyszukać (za pomocą Ctrl + F) powtórzenia nazwy danej funkcji, a więc sprawdzić, czy wywołuje sama siebie. Wśród przykładów algorytmów rekurencyjnych można wymienić ciąg Fibonacciego, silnię czy wyszukiwanie binarne.
Co to jest wywołanie rekurencyjne?
Wywołanie rekurencyjne to moment, gdy funkcja w trakcie swojego wykonania decyduje się na rozwiązanie pewnego problemu poprzez wywołanie samej siebie. Każde takie wywołanie prowadzi do podziału problemu na mniejsze podproblemy, aż do osiągnięcia wykonania elementarnego (po spełnieniu warunku brzegowego), który kończy rekurencyjne wywołania.
Wpisy, które mogą Cię zainteresować:


