ROZWIĄZANIA: Matura z informatyki - maj 2023 | Korepetycje do matury z informatyki

9 kwietnia 2024
Posted by: Damian
Category: Baza wiedzy

W tym artykule znajdziesz rozwiązania matury z informatyki w formule 2023, przy użyciu Microsoft Access (SQL), a także C++, java i python. Skorzystaj z tych informacji, dla zrozumienia jak należy wykonać poszczególne podpunkty w zadaniach. Załączniki potrzebne do wykonania poniższych zadań, możesz znaleźć pod tym linkiem.

Spis treści

1 Zadanie 1 – Biblioteczka Adama

1.1 Zadanie 1.1.

1.2 Zadanie 1.2.

1.3 Zadanie 1.3.

2 Zadanie 2 – Liczby binarne

3 Pełny kod 2.1-2.5 – implementacja w python, C++ i java

4 Zadanie 3 – Liczba Pi

5 Pełny kod 3.1-3.4 – implementacja w python, C++ i java

6 Zadanie 4 – Oceń prawdziwość podanych zdań

7 Zadanie 5 – Systemy pozycyjne

8 Zadanie 6 – Konfitury owocowe

9 Zadanie 7 – Gry planszowe

Zadanie 1 – Biblioteczka Adama

Matura z informatyki 2023 - zadanie 1 — Zadanie 1 – Biblioteczka Adama z arkusza maturalnego z informatyki maj 2023

Zadanie 1.1.

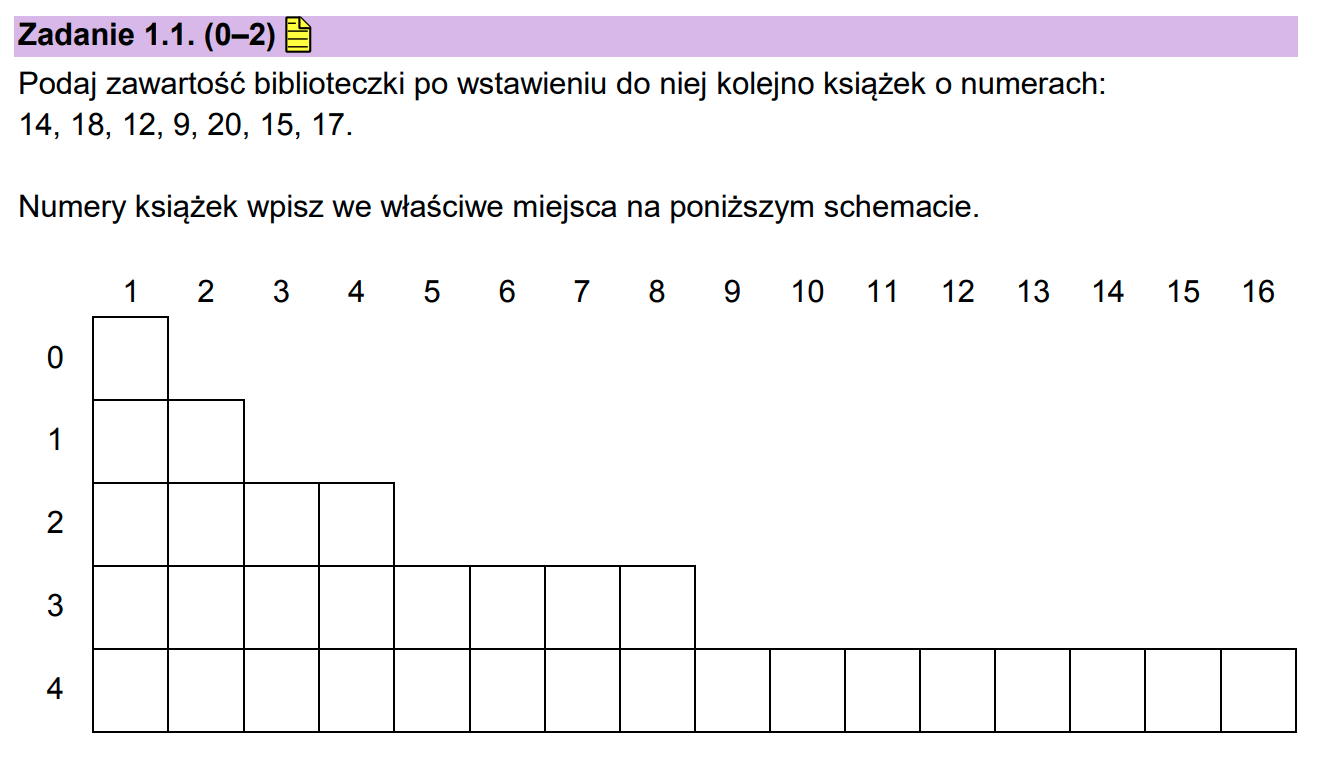
Na początku wszystkie komórki są puste i Adam zawsze zaczyna od komórki B[0,1], wstawiamy więc tam pierwszą liczbę, czyli 14.

	1	2	3	4	5	6	7	8
0	14
1
2
3

Kolejną liczbą jest 18, gdy próbujemy ją wstawić, miejsce jest już zajęte przez 14, i wybieramy opcję B[i + 1, 2j], ponieważ 18 jest większe od 14, i +1 = 1 i 2j = 2 umieszczamy więc 18 w komórce B[1,2].

	1	2
0	14
1		18
2
3

Kolejną liczbą na naszej liście jest 12, ona też nie mieści się do komórki B[0,1], ale jest ona mniejsza od liczby w tym polu, więc idzie do komórki B[i + 1, 2j – 1], czyli B[1,1].

	1	2
0	14
1	12	18
2
3

Następnie bierzemy liczbę 9, podąża ona tą samą drogą* co 12, jednak nie może zająć jej miejsca i jest od niej mniejsza, dlatego idzie kolejnym wywołaniem rekurencyjnej reguły, a następnie używając wzoru B[i + 1, 2j – 1] trafia do komórki B[2,1].

* drogą, ścieżką lub trasą będziemy nazywać warunki jakie liczba musiała spełnić, by trafić do danej komórki.

	1	2
0	14
1	12	18
2	9
3

Kolejna liczba to 20, możemy wykorzystać ścieżkę liczby 18 i dopiero tam użyć wzoru, jednak tym razem wzoru stosowanego gdy liczba jest większa czyli B[i + 1, 2j]. Tym sposobem liczba 20 trafia do komórki B[2,4].

	1	2	4
0	14
1	12	18
2	9		20
3

Liczba 15 idzie tą samą drogą co 20, z tą różnicą, że jest ona mniejsza od 18 i przez to w ostatnim wywołaniu reguły Adama wykorzystujemy wzór B[i + 1, 2j – 1] i 15 trafia do komórki B[2,3].

	1	2	3	4
0	14
1	12	18
2	9		15	20
3

Ostatnia liczba, której pozycję mamy znaleźć to 17. Wykorzystamy do tego trasę liczby 15 i dodamy jedną procedurę, używając wzoru B[i + 1, 2j] (ponieważ 17 jest większe od 15) dowiadujemy się, że miejsce 17 to B[3,6].

Rozwiązanie:

	1	2	3	4	6
0	14
1	12	18
2	9		15	20
3					17

Zadanie 1.2.

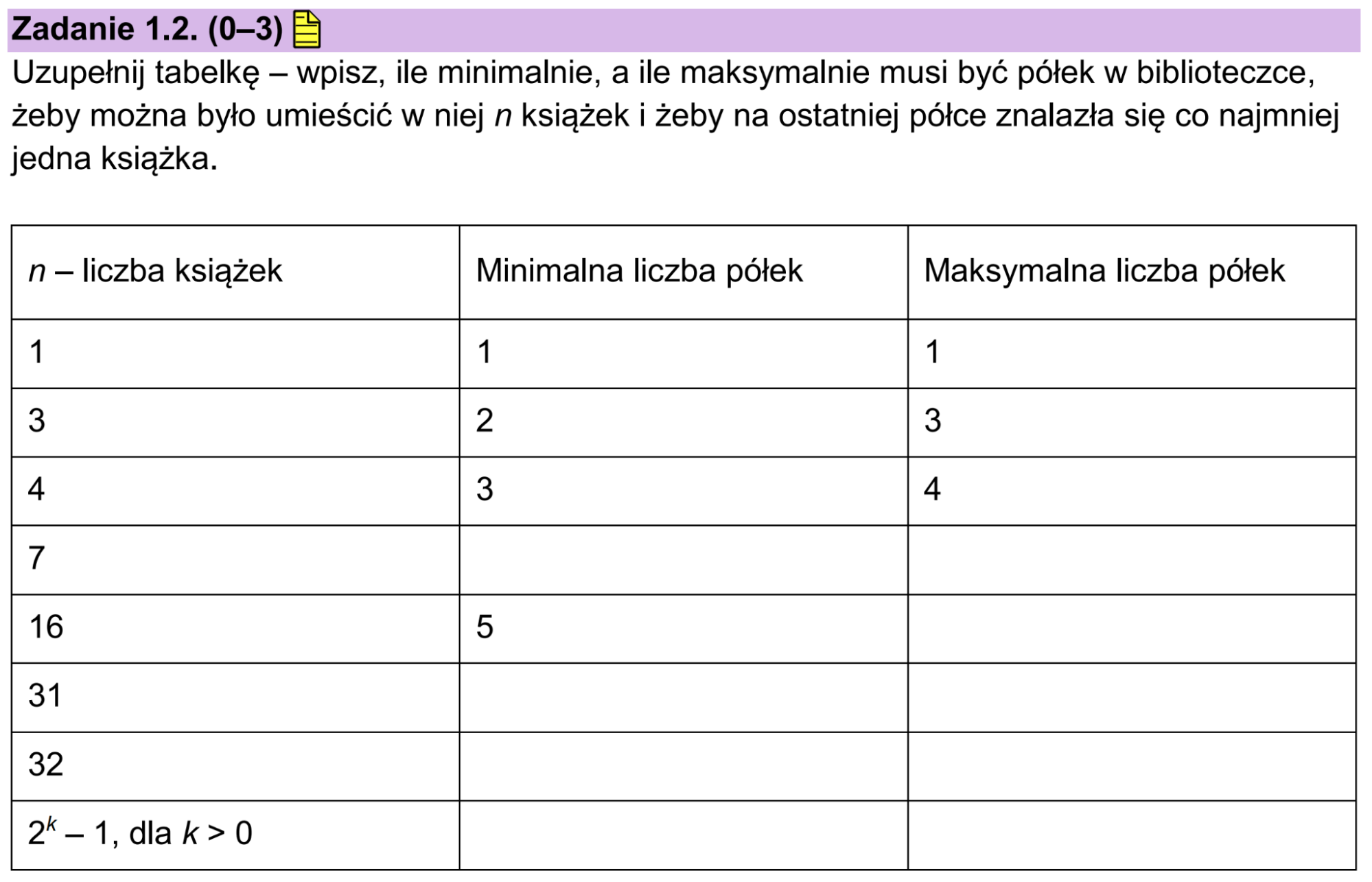
Na początek zajmiemy się maksymalną liczbą półek. Najwięcej półek to przypadek, gdy każda kolejna książka, którą wstawiamy trafia do nowej półki. Taka sytuacja ma miejsce, gdy dodawana książka zawsze ma numer większy (lub mniejszy) od poprzedniej (oczywiście poza 1 książką). Wtedy na każdej półce będzie po 1 książce (dla n książek potrzeba w takim przypadku n półek). Czyli do kolumny Maksymalna liczba półek przepisujemy po prostu wartości z kolumny n – liczba książek.

Książki będą zajmowały najmniej miejsca kiedy dla każdej z nich (oprócz tych na ostatniej półce) włożymy książkę o mniejszym (wtedy zajmiemy wolne miejsca zanim przejdziemy do następnej półki) i większym numerze identyfikacyjnym. Na przykład wkładamy trzy książki, druga i trzecia z nich będą miały mniejsze (lub większe) identyfikatory, więc zajmą 3 półki. Tylko jeśli jedna jest mniejsza, a jedna jest większa, zajmą 2.

Widzimy wtedy, że minimalną liczbą półek jaka jest potrzebna, to taka której suma przegródek wszystkich półek jest większa lub równa liczbie książek. Jeśli liczba książek przekracza liczbę wszystkich komórek musimy dodać kolejną półkę. Wystarczy, że będziemy liczyć wszystkie pola każdej kolejnej półki, aż w końcu dojdziemy do liczby książek której szukamy, należy sprawdzić wtedy numer półki i dodać 1 (półki są numerowane od 0) i otrzymaliśmy minimalną liczbę półek, Może to być jednak ciężkie dla większych liczb, poza tym i tak musimy znaleźć ogólny wzór. Szukamy więc jakiejś zależności. Zobaczmy tabelę, widać że minimalne wartości dla kolejnych liczb są bardzo bliskie wykładnikom do których musi być podniesiona 2, by osiągnąć wartości bliskie liczbie książek. Możemy policzyć logarytmy binarne (o podstawie 2) z kolejnych liczb, żeby dokładniej zbadać tę relację. Okazuje się, że wystarczy zaokrąglić uzyskany logarytm z liczby książek w dół i dodać jeden, aby otrzymać minimalną liczbę półek. Nasz wzór to ⌊log(n)⌋+1, gdzie n to liczba książek, teraz wystarczy podstawić odpowiednie wartości, policzyć je i wpisać do tabelki. W ostatniej linijce będzie to ⌊log(2ᵏ-1)⌋+1.

Rozwiązanie:

n – liczba książek	Minimalna liczba półek	Maksymalna liczba półek
1	1	1
3	2	3
4	3	4
7	3	7
16	5	16
31	5	31
32	6	32
2ᵏ-1	⌊log(2ᵏ-1)⌋+1	2ᵏ-1

Zadanie 1.3.

Warto zwizualizować sobie wywołania algorytmu na drzewie wywołań rekurencyjnych, to znacznie ułatwi wykonanie zadania. Drzewo zaczyna się od liczby w komórce B[0,1], algorytm wypisuje jej wartość i przechodzi do przegródki B[i + 1, 2j – 1] (nie jest pusta) i dopiero, gdy wykona się dla niej (i każdej komórki do której przechodzi) wraca z powrotem i wykonuje się dla komórki B[i + 1, 2j]. Oto drzewo wywołań dla podpunktu a:

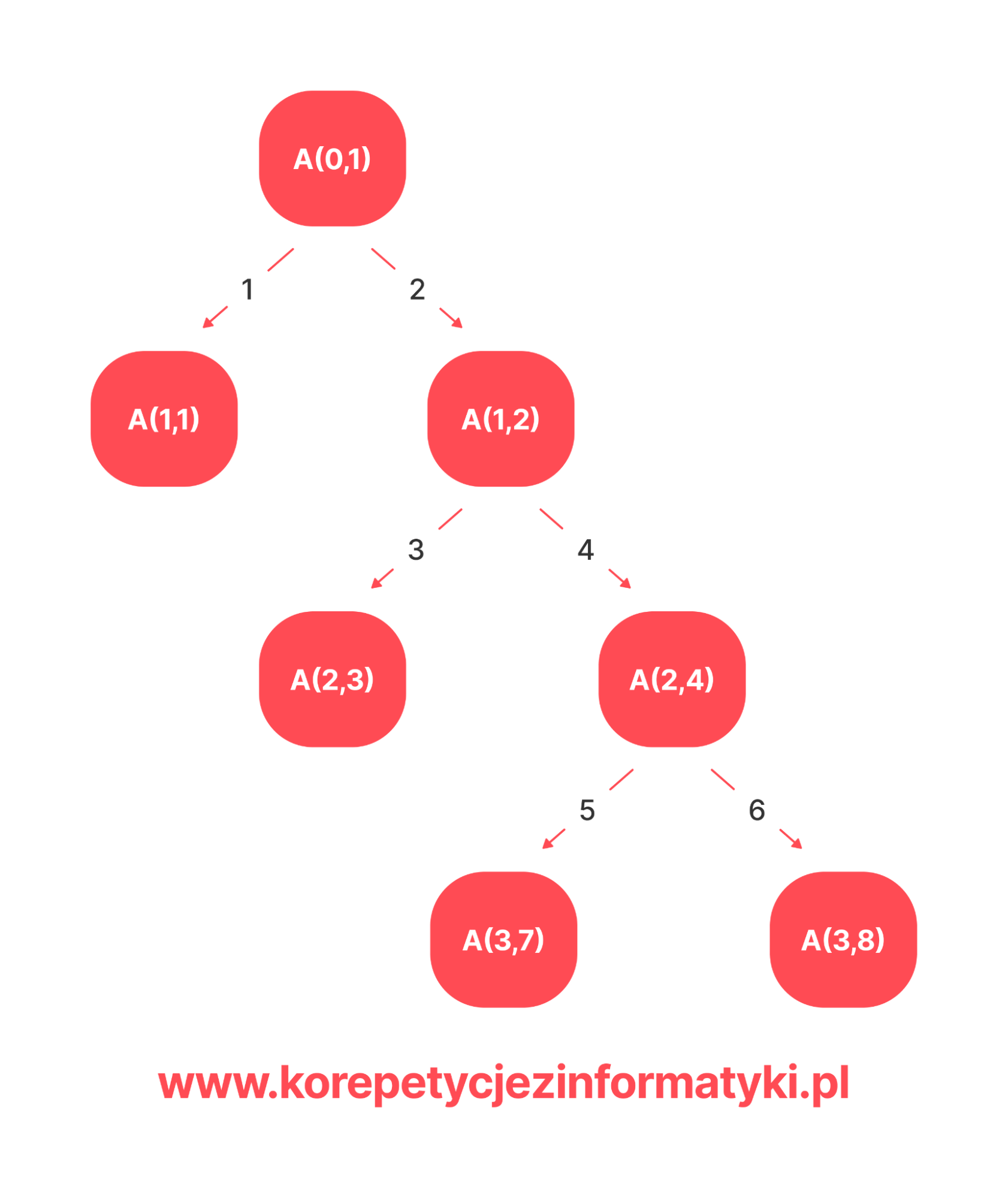
Rozwiązanie - Matura z informatyki 2023 - zadanie 1.3 a — Drzewo wywołań rekurencyjnych – podpunkt a

Wypisujemy wartość komórki B[0,1] – 9, następnie przez funkcję A(1,1) przechodzimy do komórki B[1,1] i wypisujemy 2. Z tej komórki już nie przejdziemy do żadnej komórki, więc cała funkcja została wykonana. Wracamy do funkcji A(0,1), tam jesteśmy przekierowani poprzez A(1,2) do komórki B[1,2] i wypisujemy jej wartość – 12. Zostajemy przekierowani do B[2,3] i wypisujemy – 10. W tej komórce nie ma żadnych przekierowań, więc wracamy do funkcji A(1,2), przechodzimy do przegródki B[2,4] i wypisujemy jej wartość – 14. Z tej komórki najpierw pójdziemy do przegródki B[3,7] wypiszemy jej wartość – 13 i wrócimy, bo nie ma dalej żadnych niepustych przegródek, do których moglibyśmy przejść. Zostaniemy przekierowani do komórki B[3,8], wypiszemy wartość – 15 i znowu wrócimy. Jednak nie ma już dalszych kroków, więc wracamy do poprzednich wywołań, gdzie również wszystkie instrukcje zostały wykonane.

Dochodzimy do funkcji A(0,1) i tam również wszystkie polecenia zostały wykonane, nie ma jednak gdzie powrócić co oznacza, że cały algorytm został wykonany.

Rozwiązanie:

9, 2, 12, 10, 14, 13, 15.

Przejdźmy do podpunktu b.

Drzewo wykonań rekurencyjnych wygląda tak:

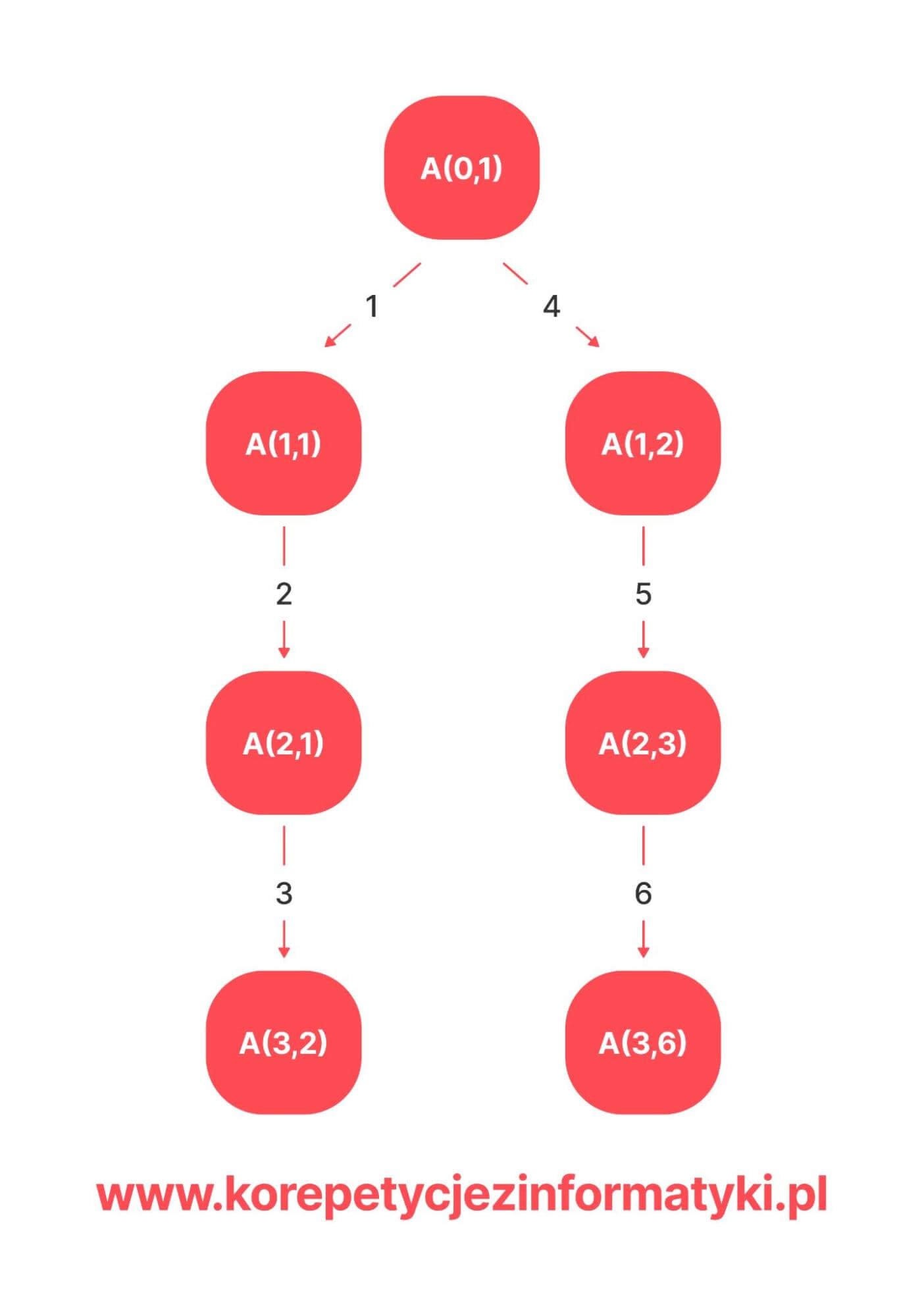
Rozwiązanie - Matura z informatyki 2023 - zadanie 1.3 b — Drzewo wywołań rekurencyjnych – podpunkt b

Znowu zaczynamy od przegródki B[0,1] – wpisujemy 10. Wywołaniem funkcji A(i + 1, 2j – 1) przechodzimy do przegródki B[1, 1] i wypisujemy wartość 8. Dalej zostajemy przekierowani funkcją A(3,2) do przegródki B[3,2] i wypisujemy wartość 6. Wracamy do funkcji A(2,1), a z niej do funkcji A(1,1), następnie do oryginalnej funkcji.

Teraz podążamy za funkcją A(1,2), wypisujemy 15 i dalej zostajemy przekierowani do przegródki B[2,3]. Wypisujemy jej wartość – 12 i przechodzimy do komórki B[3,6], tam wypisujemy 13. Teraz wracamy na samą górę naszego drzewa wywołań rekurencyjnych do funkcji A(0,1), gdzie nie ma już dalszych wywołań – algorytm zakończy zadanie.

Rozwiązanie:

10, 8, 4, 6, 15, 12, 13.

Zadanie 2 – Liczby binarne

Matura z informatyki 2023 - zadanie 2 — Zadanie 2 – Liczby binarne z arkusza maturalnego z informatyki maj 2023

Zadanie 2.1.

Żeby napisać algorytm zajmujący się tym problemem, należy znać właściwości operatorów dzielenia całkowitego (div) oraz reszty z dzielenia – modulo (mod).

Dzielenie całkowite sprawia, że odrzuca się pozostałą resztę po wykonaniu dzielenia. Przykładowo 222 div 10 równa się 22.

Reszta z dzielenia tak jak sama nazwa wskazuje zwraca samą resztę pozostałą po dzieleniu. Dla działania 222 mod 10 otrzymujemy wynik 2 (222/10 to 22 z resztą równą 2).

Najlepszym sposobem na rozwiązanie problemu jest zwrócenie uwagi, czy każda kolejna cyfra (oprócz pierwszej) jest inna niż poprzednia. Jeśli cyfra okazuje się różna, to znaczy, że jest to nowy blok i należy zwiększyć licznik bloków – b. Należy ustawić wartość początkową wartość b na 1, ponieważ opisany sposób nie liczy pierwszego (nie ma przecież bloku 0 z którym moglibyśmy go porównać). Żeby uzyskać kolejne cyfry liczby n użyjemy mod 2, a następnie podzielimy ją przez 2 żeby przejść do kolejnej cyfry. Użyjemy też zmiennej pomocniczej poprzednia, która będzie zapisywała poprzednią cyfrę.

b ← 1
poprzednia ← n mod 2
n ← n div 2
dopóki (n > 0)
    cyfra ← n mod 2
        jeżeli cyfra ≠ poprzednia
            b ← b + 1
        poprzednia ← cyfra
    n ← n div 2

b ← 1

poprzednia ← n mod 2

n ← n div 2

dopóki (n > 0)

cyfra ← n mod 2

jeżeli cyfra ≠ poprzednia

b ← b + 1

poprzednia ← cyfra

n ← n div 2

Dla sprawdzenia możemy napisać nasz program w pythonie (lub innym języku) i zobaczyć, czy zwraca poprawne wyniki.

Implementacja – Python

def liczbaBlokow(n):
    b = 1
    poprzednia = n % 2
    n //= 2
    while n > 0:
        cyfra = n % 2
        if cyfra != poprzednia:
            b += 1
        poprzednia = cyfra
        n //= 2
    return b

def liczbaBlokow(n):

b = 1

poprzednia = n % 2

n //= 2

while n > 0:

cyfra = n % 2

if cyfra != poprzednia:

b += 1

poprzednia = cyfra

n //= 2

return b

Implementacja – C++

int liczbaBlokow(int n) {
    int b = 1;
    int poprzednia = n % 2;
    n /= 2;
    while (n > 0) {
        int cyfra = n % 2;
        if (cyfra != poprzednia) {
            b++;
        }
        poprzednia = cyfra;
        n /= 2;
    }
    return b;
}

int liczbaBlokow(int n) {

int b = 1;

int poprzednia = n % 2;

n /= 2;

while (n > 0) {

int cyfra = n % 2;

if (cyfra != poprzednia) {

b++;

}

poprzednia = cyfra;

n /= 2;

}

return b;

}

Implementacja – Java

public static int liczbaBlokow(int n) {
    int b = 1;
    int poprzednia = n % 2;
    n /= 2;
    while (n > 0) {
        int cyfra = n % 2;
        if (cyfra != poprzednia) {
            b++;
        }
        poprzednia = cyfra;
        n /= 2;
    }
    return b;
}

public static int liczbaBlokow(int n) {

int b = 1;

int poprzednia = n % 2;

n /= 2;

while (n > 0) {

int cyfra = n % 2;

if (cyfra != poprzednia) {

b++;

}

poprzednia = cyfra;

n /= 2;

}

return b;

}

Matura z informatyki 2023 - informacja do zadań 2.2 i 2.3 — Informacja do zadań 2.2. i 2.3.

W kolejnych podpunktach mamy do czynienia już z liczbami w systemie dwójkowym, wypadałoby więc dostosować naszą funkcję. Jednak zamiast tego możemy po prostu zamienić je na liczby dziesiętne, okazuje się to znacznie szybsze niż zmienianie funkcji. Jest to z pewnością rozwiązanie mniej zoptymalizowane jednak na maturze liczy się czas pisania programów, a nie ich wydajność.

Implementacja – Python

with open("bin.txt","r") as plik:
    linie = plik.readlines()
    for i in range(len(linie)):
        linie[i] = int(linie[i].rstrip(),2)

with open("bin.txt","r") as plik:

linie = plik.readlines()

for i in range(len(linie)):

linie[i] = int(linie[i].rstrip(),2)

Teraz w liście linie znajdują się liczby w systemie 10. Porównując długość powyższego kodu z poniższymi, możesz się zorientować dlaczego Python jest preferowany na maturze.

Implementacja – C++

Biblioteki:

#include <iostream>
#include <fstream>
#include <string>

#include <iostream>

#include <fstream>

#include <string>

Kod:

#include <iostream>
#include <fstream>
#include <string>
using namespace std;
int main(){
    ifstream plik("bin.txt"); // Otwarcie pliku do odczytu 
    if (plik.is_open()) {
        int linie[100]; 
        string line;
        int count = 0;
   
        // Odczyt i konwersja linii z pliku
        while (getline(plik, line)) {
            linie[count++] = stoi(line, nullptr, 2); // Konwersja z systemu binarnego na dziesiętny. Funkcja stoi służy do konwersji ciągu znaków na liczbę całkowitą typu int.
        }
    
        for (int i = 0; i < count; ++i) {
            cout << linie[i] << endl; // Wyświetlenie przekonwertowanych wartości - dla przykladu
        }
    } else {
        cerr << "Nie można otworzyć pliku." << endl;
    }
}

#include <iostream>

#include <fstream>

#include <string>

using namespace std;

int main(){

ifstream plik("bin.txt"); // Otwarcie pliku do odczytu

if (plik.is_open()) {

int linie[100];

string line;

int count = 0;

// Odczyt i konwersja linii z pliku

while (getline(plik, line)) {

linie[count++] = stoi(line, nullptr, 2); // Konwersja z systemu binarnego na dziesiętny. Funkcja stoi służy do konwersji ciągu znaków na liczbę całkowitą typu int.

}

for (int i = 0; i < count; ++i) {

cout << linie[i] << endl; // Wyświetlenie przekonwertowanych wartości - dla przykladu

}

} else {

cerr << "Nie można otworzyć pliku." << endl;

}

Implementacja – Java

Biblioteki:

import java.io.BufferedReader;
import java.io.FileReader;

1 2	import java.io.BufferedReader; import java.io.FileReader;

Kod:

String fileName = "bin.txt";
int[] linie = null;
BufferedReader plik = null; // Obiekt do odczytu pliku

// Otwarcie pliku do odczytu
plik = new BufferedReader(new FileReader(fileName));

int count = 100; // Ilość linii w pliku
String line;

// Ponowne otwarcie pliku, aby odczytać jego zawartość
plik = new BufferedReader(new FileReader(fileName));
linie = new int[count];
int i = 0;

while ((line = plik.readLine()) != null) {
    linie[i] = Integer.parseInt(line.trim(), 2); // Konwersja ciągu znaków na liczbę całkowitą w systemie binarnym
    i++;
}

// Zamknięcie obiektu BufferedReader po zakończeniu odczytu
if (plik != null) {
    plik.close();
}

// Wyświetlenie przekonwertowanych wartości - dla przykładu
if (linie != null) {
    for (int value : linie) {
        System.out.println(value);
    }
}

String fileName = "bin.txt";

int[] linie = null;

BufferedReader plik = null; // Obiekt do odczytu pliku

// Otwarcie pliku do odczytu

plik = new BufferedReader(new FileReader(fileName));

int count = 100; // Ilość linii w pliku

String line;

// Ponowne otwarcie pliku, aby odczytać jego zawartość

plik = new BufferedReader(new FileReader(fileName));

linie = new int[count];

int i = 0;

while ((line = plik.readLine()) != null) {

linie[i] = Integer.parseInt(line.trim(), 2); // Konwersja ciągu znaków na liczbę całkowitą w systemie binarnym

i++;

}

// Zamknięcie obiektu BufferedReader po zakończeniu odczytu

if (plik != null) {

plik.close();

}

// Wyświetlenie przekonwertowanych wartości - dla przykładu

if (linie != null) {

for (int value : linie) {

System.out.println(value);

}

Zadanie 2.2.

Implementacja – Python

licznik = 0
for liczba in linie:
    if liczbaBlokow(liczba)<=2:
        licznik += 1
print(licznik)

licznik = 0

for liczba in linie:

if liczbaBlokow(liczba)<=2:

licznik += 1

print(licznik)

Implementacja – C++

int licznik = 0;
int rozmiar_tablicy = 100 // rozmiar tablicy, bo plik bin posiada 100 wierszy
for (int liczba = 0; i < rozmiar_tablicy; liczba++) {
    if (liczbaBlokow(linie[i]) <= 2) {
        licznik++;
    }
}
cout << licznik << endl;

int licznik = 0;

int rozmiar_tablicy = 100 // rozmiar tablicy, bo plik bin posiada 100 wierszy

for (int liczba = 0; i < rozmiar_tablicy; liczba++) {

if (liczbaBlokow(linie[i]) <= 2) {

licznik++;

}

cout << licznik << endl;

Implementacja – Java

int licznik = 0;
int rozmiar_tablicy = 100; // rozmiar tablicy, bo plik bin posiada 100 wierszy
for (int liczba = 0; liczba < rozmiar_tablicy; liczba++) {
    if (liczbaBlokow(linie[liczba]) <= 2) {
        licznik++;
    }
}

int licznik = 0;

int rozmiar_tablicy = 100; // rozmiar tablicy, bo plik bin posiada 100 wierszy

for (int liczba = 0; liczba < rozmiar_tablicy; liczba++) {

if (liczbaBlokow(linie[liczba]) <= 2) {

licznik++;

}

Rozwiązanie:

Zadanie 2.3.

Możemy tutaj użyć funkcji max (w języku python), zamiast manualnie szukać liczby.

Odpowiedź musi być w systemie binarnym, więc trzeba przekonwertować liczbę na ten system.

Implementacja – Python

maksymalna = bin(max(linie))
print(maksymalna.lstrip("0b"))

1 2	maksymalna = bin(max(linie)) print(maksymalna.lstrip("0b"))

Implementacja – C++

Biblioteki:

#include <iostream>
#include <algorithm> // Biblioteka zawierająca funkcje algorytmiczne, w tym max_element
#include <bitset> // Biblioteka zawierająca klasę std::bitset, która reprezentuje sekwencję bitów

#include <iostream>

#include <algorithm> // Biblioteka zawierająca funkcje algorytmiczne, w tym max_element

#include <bitset> // Biblioteka zawierająca klasę std::bitset, która reprezentuje sekwencję bitów

Kod główny:

int maksymalna = *max_element(linie, linie + count); // Znalezienie maksymalnej wartości w tablicy i konwersja na binarną
string maksymalna_str = bitset<32>(maksymalna).to_string(); // Konwersja liczby binarnej na ciąg znaków
cout << maksymalna_str.erase(0, maksymalna_str.find_first_not_of('0')) << endl; // Usunięcie wiodących zer i wyświetlenie wyniku

int maksymalna = *max_element(linie, linie + count); // Znalezienie maksymalnej wartości w tablicy i konwersja na binarną

string maksymalna_str = bitset<32>(maksymalna).to_string(); // Konwersja liczby binarnej na ciąg znaków

cout << maksymalna_str.erase(0, maksymalna_str.find_first_not_of('0')) << endl; // Usunięcie wiodących zer i wyświetlenie wyniku

Implementacja – Java

Biblioteki:

import java.util.Arrays;

1	import java.util.Arrays;

Kod główny:

int maksymalna = Arrays.stream(linie).max().getAsInt();  // Znalezienie maksymalnej wartości w tablicy linie
String maksymalna_str = Integer.toBinaryString(maksymalna).replaceFirst("^0b", ""); // Konwersja na postać binarną i usunięcie początkowych "0b"
System.out.println(maksymalna_str); // Wyświetlenie wyniku

int maksymalna = Arrays.stream(linie).max().getAsInt(); // Znalezienie maksymalnej wartości w tablicy linie

String maksymalna_str = Integer.toBinaryString(maksymalna).replaceFirst("^0b", ""); // Konwersja na postać binarną i usunięcie początkowych "0b"

System.out.println(maksymalna_str); // Wyświetlenie wyniku

Rozwiązanie:

1110100011100011100

Zadanie 2.4.

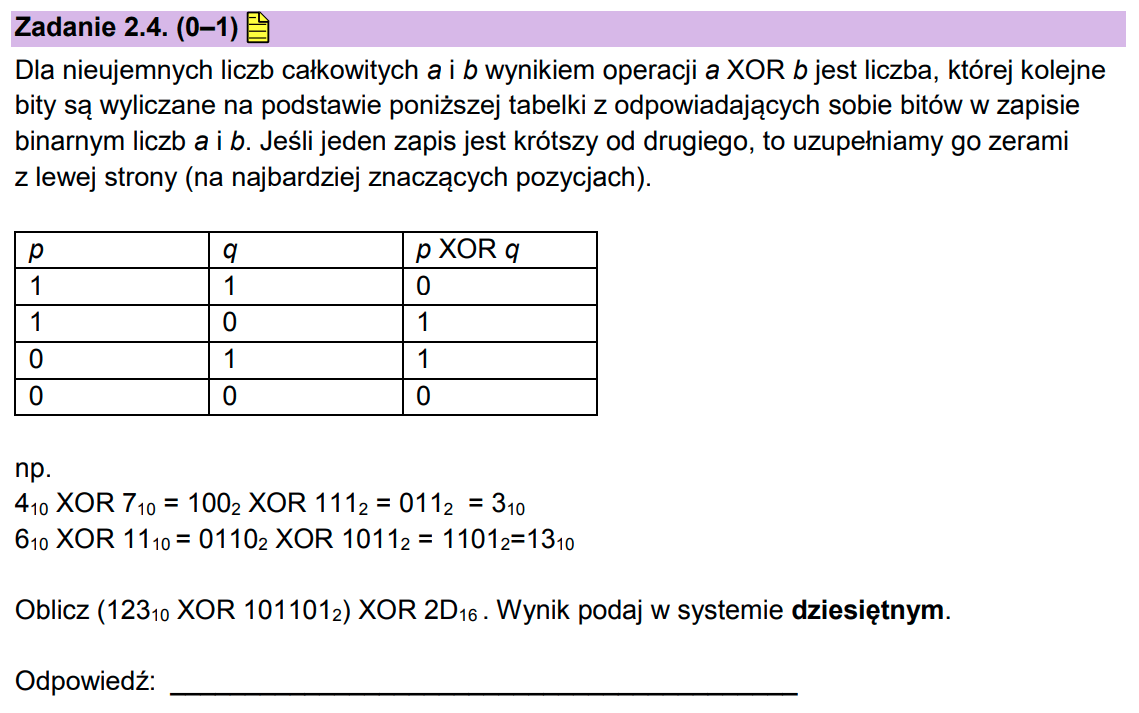
Najpierw musimy przekonwertować 123₁₀ na system binarny.

123₁₀ = 1111011₂

Teraz do liczby o mniejszej liczbie cyfr należy dodać tyle 0 z przodu, żeby liczba cyfr obydwu liczb była równa.

1111011₂

0101101₂

_______

1010110₂

Teraz należy przekonwertować 2D na system dwójkowy. 2D = 101101₂. Znowu dodajemy wiodące 0 i liczymy XOR.

1010110₂

0101101₂

_______

1111011₂

Teraz wystarczy przekonwertować wynik na system dziesiętny i odpowiedź jest gotowa: 1111011₂ = 123₁₀

Zamiast robić wszystkie operacje ręcznie możemy użyć dostępnych w pythonie (lub w innych językach) funkcji.

Implementacja – Python

Najpierw należałoby przekonwertować wszystkie liczby na system dziesiętny funkcją int(“liczba”,baza), a potem użyć operatora ^, aby otrzymać XOR dwóch liczb.

print((123^int("101101",2))^int("2D",16))

1	print((123^int("101101",2))^int("2D",16))

Implementacja – C++

Biblioteki:

#include <iostream>
#include <bitset>
#include <string>

#include <iostream>

#include <bitset>

#include <string>

Kod:

int rezultat = 123 ^ stoi("101101", nullptr, 2) ^ stoi("2D", nullptr, 16); // Wyrażenie bitowe XOR na liczbach w różnych systemach liczbowych.
cout << rezultat << endl;

1 2	int rezultat = 123 ^ stoi("101101", nullptr, 2) ^ stoi("2D", nullptr, 16); // Wyrażenie bitowe XOR na liczbach w różnych systemach liczbowych. cout << rezultat << endl;

Implementacja – Java

int rezultat = (123 ^ Integer.parseInt("101101", 2)) ^ Integer.parseInt("2D", 16); // Wyrażenie bitowe XOR na liczbach w różnych systemach liczbowych
System.out.println(rezultat); // Wyświetlenie wyniku

1 2	int rezultat = (123 ^ Integer.parseInt("101101", 2)) ^ Integer.parseInt("2D", 16); // Wyrażenie bitowe XOR na liczbach w różnych systemach liczbowych System.out.println(rezultat); // Wyświetlenie wyniku

Rozwiązanie:

123

Zadanie 2.5.

Operacja XOR jest dostępna natywnie w pythonie, reprezentuje ją symbol ^. Działa ona na dwóch liczbach dziesiętnych i zwraca również liczbę dziesiętną, wynik więc trzeba będzie przekonwertować. Oczywiście odpowiedź należy skopiować do pliku wyniki2_5.txt, a kod do innego dokumentu tekstowego.

Implementacja – Python

for liczba in linie:
    print(bin(liczba^liczba//2).lstrip("0b"))

1 2	for liczba in linie: print(bin(liczba^liczba//2).lstrip("0b"))

Implementacja – C++

Biblioteki:

#include <iostream>
#include <bitset>

1 2	#include <iostream> #include <bitset>

Kod:

for (int i = 0; i < n; i++) {
    // Wyrażenie bitowe XOR na liczbie i jej połowie, konwersja na binarną i usunięcie wiodących zer
    cout << bitset<32>(linie[i] ^ (linie[i] / 2)).to_string().erase(0, bitset<32>(linie[i] ^ (linie[i] / 2)).to_string().find_first_not_of('0')) << endl;
}

for (int i = 0; i < n; i++) {

// Wyrażenie bitowe XOR na liczbie i jej połowie, konwersja na binarną i usunięcie wiodących zer

cout << bitset<32>(linie[i] ^ (linie[i] / 2)).to_string().erase(0, bitset<32>(linie[i] ^ (linie[i] / 2)).to_string().find_first_not_of('0')) << endl;

}

Implementacja – Java

Biblioteki:

import java.util.Arrays;

1	import java.util.Arrays;

Kod:

for (int liczba: linie) {
    System.out.println(Integer.toBinaryString(liczba ^ (liczba / 2)).replaceFirst("^0b", "")); // Wyrażenie bitowe XOR na liczbie i jej połowie, konwersja na postać binarną i usunięcie początkowych "0b"
}

for (int liczba: linie) {

System.out.println(Integer.toBinaryString(liczba ^ (liczba / 2)).replaceFirst("^0b", "")); // Wyrażenie bitowe XOR na liczbie i jej połowie, konwersja na postać binarną i usunięcie początkowych "0b"

}

Rozwiązanie:

1001011000

1111000001

1110001000

1101100001111010

110100010

1100110000110000

100010000

1110111101

1100110011

1110001100001

111110111101000

100110100011010

1000001000

11101010110100010

11101101111

1100001010101010

10011110101

1101000111100010001

1010000101110010

11101100000

1000000000

100000010010

1100010

11010011

110110000001000

1000010

10100111001001

1100011101111

101010110001

1001100100001111

100110000111

110100110011110111

111000110110110011

10100111101010

1111000110011000

101111110101

1110011111111011

11010110100100100

110000000

1000000110010011

1001111100001

1111011101

11000000100

10000101000011110

10100010111101

110001000

111101100011001

100110000

1101101011110100

110110101111

101110111001000100

1110110000100111

1011001010011

100000000

1111110111100

11011110111001

110110101110000110

1101101000111101

111100010

100111010111001

110000010100

1010111011

1001110010010010010

101100111101

1010110011111100111

1101010101000

111110101011100

10000000

11010111000

11001110100

1010000011010111111

110110100101

11101100000110

1011110010101000000

1001010001010010

10101100111

10000101101

100101000010

110011000100

10010110010110

101010010111001

1100011110

1011100110001011110

101001110111001

10011000101101011

10000000

11110110010101011

1101011010110

1100010010111001

11010001001100011

1010101001001

100000000

1100010010010

1111100011000

1011111011110100

11100101101110101

110001011011011

1011000101011000000

11001011110011000

Pełny kod 2.1-2.5 – implementacja w python, C++ i java

Implementacja – Python

# oblicza liczbę bloków 1-bitowych w zapisie binarnym liczby n. Iteruje przez kolejne bity liczby, zliczając zmiany wartości bitu
def liczbaBlokow(n):
    b = 1
    poprzednia = n % 2
    n //= 2
    while n > 0:
        cyfra = n % 2
        if cyfra != poprzednia:
            b += 1
        poprzednia = cyfra  # zmiana poprzedniej, tylko gdy cyfra się różni
        n //= 2
    return b

# odczyt i konwersja danych z pliku
with open("bin.txt","r") as plik:
    linie = plik.readlines()
    for i in range(len(linie)):
        linie[i] = int(linie[i].rstrip(),2)

# liczenie liczby elementów z liczbami, które mają co najwyżej 2 bloki 1-bitowych
licznik = 0
for liczba in linie:
    if liczbaBlokow(liczba)<=2:
        licznik += 1
print(licznik)

# obliczenie i wyświetlenie maksymalnej wartości z listy linie w postaci binarnej (dwójkowej)
maksymalna = bin(max(linie))
print(maksymalna.lstrip("0b"))

# wykonanie operacji bitowej XOR na liczbach 123, 0b101101 (185 w systemie dziesiętnym) i 0x2D (45 w systemie dziesiętnym) oraz wyświetlenie wyniku
print((123^int("101101",2))^int("2D",16))

# wyświetlenie wyniku operacji bitowej XOR na liczbie i jej połowie w postaci binarnej dla każdej liczby z listy linie
for liczba in linie:
    print(bin(liczba^liczba//2).lstrip("0b"))

# oblicza liczbę bloków 1-bitowych w zapisie binarnym liczby n. Iteruje przez kolejne bity liczby, zliczając zmiany wartości bitu

def liczbaBlokow(n):

b = 1

poprzednia = n % 2

n //= 2

while n > 0:

cyfra = n % 2

if cyfra != poprzednia:

b += 1

poprzednia = cyfra # zmiana poprzedniej, tylko gdy cyfra się różni

n //= 2

return b

# odczyt i konwersja danych z pliku

with open("bin.txt","r") as plik:

linie = plik.readlines()

for i in range(len(linie)):

linie[i] = int(linie[i].rstrip(),2)

# liczenie liczby elementów z liczbami, które mają co najwyżej 2 bloki 1-bitowych

licznik = 0

for liczba in linie:

if liczbaBlokow(liczba)<=2:

licznik += 1

print(licznik)

# obliczenie i wyświetlenie maksymalnej wartości z listy linie w postaci binarnej (dwójkowej)

maksymalna = bin(max(linie))

print(maksymalna.lstrip("0b"))

# wykonanie operacji bitowej XOR na liczbach 123, 0b101101 (185 w systemie dziesiętnym) i 0x2D (45 w systemie dziesiętnym) oraz wyświetlenie wyniku

print((123^int("101101",2))^int("2D",16))

# wyświetlenie wyniku operacji bitowej XOR na liczbie i jej połowie w postaci binarnej dla każdej liczby z listy linie

for liczba in linie:

print(bin(liczba^liczba//2).lstrip("0b"))

Implementacja – C++

#include <iostream>
#include <fstream>
#include <string>
#include <algorithm> // Biblioteka zawierająca funkcje algorytmiczne, w tym max_element
#include <bitset> // Biblioteka zawierająca klasę std::bitset, która reprezentuje sekwencję bitów

using namespace std;

// Funkcja liczbaBlokow zlicza liczbę bloków 1-bitowych w liczbie n
int liczbaBlokow(int n) {
    int b = 1;
    int poprzednia = n % 2;
    n /= 2;
    while (n > 0) {
        int cyfra = n % 2;
        if (cyfra != poprzednia) {
            b++;
        }
        poprzednia = cyfra;
        n /= 2;
    }
    return b;
}

int main() {
    ifstream plik("bin.txt"); // Otwarcie pliku do odczytu 
    if (plik.is_open()) {
        int linie[100]; 
        string line;
        int count = 0;
   
        // Odczyt i konwersja linii z pliku
        while (getline(plik, line)) {
            linie[count++] = stoi(line, nullptr, 2); // Konwersja z systemu binarnego na dziesiętny. Funkcja stoi służy do konwersji ciągu znaków na liczbę całkowitą typu int.
        }

        // Obliczenie liczby elementów w tablicy
        int rozmiar_tablicy = 100; // rozmiar tablicy, bo plik bin posiada 100 wierszy
        int licznik = 0;
        for (int liczba = 0; liczba < rozmiar_tablicy; liczba++) {
            if (liczbaBlokow(linie[liczba]) <= 2) {
                licznik++;
            }
        }
        cout << licznik << endl;

        // Obliczenie i wyświetlenie maksymalnej wartości z tablicy w postaci binarnej
        int maksymalna = *max_element(linie, linie + count);
        string maksymalna_str = bitset<32>(maksymalna).to_string();
        cout << maksymalna_str.erase(0, maksymalna_str.find_first_not_of('0')) << endl;

        // Obliczenie i wyświetlenie wyniku operacji bitowej XOR na liczbach
        int rezultat = (123 ^ bitset<6>("101101").to_ulong()) ^ stoi("2D", nullptr, 16);
        cout << rezultat << endl;

        // Wyświetlenie wyniku operacji bitowej XOR na liczbie i jej połowie dla każdej liczby z tablicy
        for (int i = 0; i < count; i++) {
            cout << bitset<32>(linie[i] ^ (linie[i] / 2)).to_string().erase(0, bitset<32>(linie[i] ^ (linie[i] / 2)).to_string().find_first_not_of('0')) << endl;
        }

    } else {
        cerr << "Nie można otworzyć pliku." << endl;
    }

    return 0;
}

#include <iostream>

#include <fstream>

#include <string>

#include <algorithm> // Biblioteka zawierająca funkcje algorytmiczne, w tym max_element

#include <bitset> // Biblioteka zawierająca klasę std::bitset, która reprezentuje sekwencję bitów

using namespace std;

// Funkcja liczbaBlokow zlicza liczbę bloków 1-bitowych w liczbie n

int liczbaBlokow(int n) {

int b = 1;

int poprzednia = n % 2;

n /= 2;

while (n > 0) {

int cyfra = n % 2;

if (cyfra != poprzednia) {

b++;

}

poprzednia = cyfra;

n /= 2;

}

return b;

}

int main() {

ifstream plik("bin.txt"); // Otwarcie pliku do odczytu

if (plik.is_open()) {

int linie[100];

string line;

int count = 0;

// Odczyt i konwersja linii z pliku

while (getline(plik, line)) {

linie[count++] = stoi(line, nullptr, 2); // Konwersja z systemu binarnego na dziesiętny. Funkcja stoi służy do konwersji ciągu znaków na liczbę całkowitą typu int.

}

// Obliczenie liczby elementów w tablicy

int rozmiar_tablicy = 100; // rozmiar tablicy, bo plik bin posiada 100 wierszy

int licznik = 0;

for (int liczba = 0; liczba < rozmiar_tablicy; liczba++) {

if (liczbaBlokow(linie[liczba]) <= 2) {

licznik++;

}

cout << licznik << endl;

// Obliczenie i wyświetlenie maksymalnej wartości z tablicy w postaci binarnej

int maksymalna = *max_element(linie, linie + count);

string maksymalna_str = bitset<32>(maksymalna).to_string();

cout << maksymalna_str.erase(0, maksymalna_str.find_first_not_of('0')) << endl;

// Obliczenie i wyświetlenie wyniku operacji bitowej XOR na liczbach

int rezultat = (123 ^ bitset<6>("101101").to_ulong()) ^ stoi("2D", nullptr, 16);

cout << rezultat << endl;

// Wyświetlenie wyniku operacji bitowej XOR na liczbie i jej połowie dla każdej liczby z tablicy

for (int i = 0; i < count; i++) {

cout << bitset<32>(linie[i] ^ (linie[i] / 2)).to_string().erase(0, bitset<32>(linie[i] ^ (linie[i] / 2)).to_string().find_first_not_of('0')) << endl;

}

} else {

cerr << "Nie można otworzyć pliku." << endl;

}

return 0;

}

Implementacja – Java

import java.io.BufferedReader;
import java.io.FileReader;
import java.io.IOException;
import java.util.Arrays;

public class Main {
    public static void main(String[] args) {
        try {
            String fileName = "bin.txt";
            int[] linie = null;
            BufferedReader plik = null; // Obiekt do odczytu pliku

            // Otwarcie pliku do odczytu
            plik = new BufferedReader(new FileReader(fileName));

            int count = 100; // Ilość linii w pliku
            String line;

            // Ponowne otwarcie pliku, aby odczytać jego zawartość
            plik = new BufferedReader(new FileReader(fileName));
            linie = new int[count];
            int i = 0;

            while ((line = plik.readLine()) != null) {
                linie[i] = Integer.parseInt(line.trim(), 2); // Konwersja ciągu znaków na liczbę całkowitą w systemie binarnym
                i++;
            }

            // Zamknięcie obiektu BufferedReader po zakończeniu odczytu
            if (plik != null) {
                plik.close();
            }

            // Sprawdzenie ile wartości ma mniej niż 2 bloki
            int licznik = 0;
            int rozmiar_tablicy = 100; // rozmiar tablicy, bo plik bin posiada 100 wierszy
            for (int liczba = 0; liczba < rozmiar_tablicy; liczba++) {
                if (liczbaBlokow(linie[liczba]) <= 2) {
                    licznik++;
                }
            }
            System.out.println(licznik);

            // Znalezienie maksymalnej wartości w tablicy linie i konwersja na postać binarną
            int maksymalna = Arrays.stream(linie).max().getAsInt();
            String maksymalna_str = Integer.toBinaryString(maksymalna).replaceFirst("^0b", "");
            System.out.println(maksymalna_str);

            // Wyrażenie bitowe XOR na liczbach w różnych systemach liczbowych i wyświetlenie wyniku
            int rezultat = (123 ^ Integer.parseInt("101101", 2)) ^ Integer.parseInt("2D", 16);
            System.out.println(rezultat);
       	 
            // Wyrażenie bitowe XOR na liczbie i jej połowie, konwersja na postać binarną i usunięcie początkowych "0b"
            for (int liczba : linie) {
                System.out.println(Integer.toBinaryString(liczba ^ (liczba / 2)).replaceFirst("^0b", ""));
            }

        } catch (IOException e) {
            e.printStackTrace();
        }
    }

	// Funkcja obliczająca liczbę bloków w liczbie binarnej
    public static int liczbaBlokow(int n) {
        int b = 1;
        int poprzednia = n % 2;
        n /= 2;
        while (n > 0) {
            int cyfra = n % 2;
            if (cyfra != poprzednia) {
                b++;
            }
            poprzednia = cyfra;
            n /= 2;
        }
        return b;
    }
}

import java.io.BufferedReader;

import java.io.FileReader;

import java.io.IOException;

import java.util.Arrays;

public class Main {

public static void main(String[] args) {

try {

String fileName = "bin.txt";

int[] linie = null;

BufferedReader plik = null; // Obiekt do odczytu pliku

// Otwarcie pliku do odczytu

plik = new BufferedReader(new FileReader(fileName));

int count = 100; // Ilość linii w pliku

String line;

// Ponowne otwarcie pliku, aby odczytać jego zawartość

plik = new BufferedReader(new FileReader(fileName));

linie = new int[count];

int i = 0;

while ((line = plik.readLine()) != null) {

linie[i] = Integer.parseInt(line.trim(), 2); // Konwersja ciągu znaków na liczbę całkowitą w systemie binarnym

i++;

}

// Zamknięcie obiektu BufferedReader po zakończeniu odczytu

if (plik != null) {

plik.close();

}

// Sprawdzenie ile wartości ma mniej niż 2 bloki

int licznik = 0;

int rozmiar_tablicy = 100; // rozmiar tablicy, bo plik bin posiada 100 wierszy

for (int liczba = 0; liczba < rozmiar_tablicy; liczba++) {

if (liczbaBlokow(linie[liczba]) <= 2) {

licznik++;

}

System.out.println(licznik);

// Znalezienie maksymalnej wartości w tablicy linie i konwersja na postać binarną

int maksymalna = Arrays.stream(linie).max().getAsInt();

String maksymalna_str = Integer.toBinaryString(maksymalna).replaceFirst("^0b", "");

System.out.println(maksymalna_str);

// Wyrażenie bitowe XOR na liczbach w różnych systemach liczbowych i wyświetlenie wyniku

int rezultat = (123 ^ Integer.parseInt("101101", 2)) ^ Integer.parseInt("2D", 16);

System.out.println(rezultat);

// Wyrażenie bitowe XOR na liczbie i jej połowie, konwersja na postać binarną i usunięcie początkowych "0b"

for (int liczba : linie) {

System.out.println(Integer.toBinaryString(liczba ^ (liczba / 2)).replaceFirst("^0b", ""));

}

} catch (IOException e) {

e.printStackTrace();

}

// Funkcja obliczająca liczbę bloków w liczbie binarnej

public static int liczbaBlokow(int n) {

int b = 1;

int poprzednia = n % 2;

n /= 2;

while (n > 0) {

int cyfra = n % 2;

if (cyfra != poprzednia) {

b++;

}

poprzednia = cyfra;

n /= 2;

}

return b;

}

Zadanie 3 – Liczba Pi

Matura z informatyki 2023 - zadanie 3 — Zadanie 3 – Liczba Pi z arkusza maturalnego z informatyki maj 2023

Zadanie 3.1.

Zadania związane z programowaniem są zazwyczaj podobne. Przede wszystkim warto pamiętać o przykładowym pliku, dzięki któremu będzie wiadomo czy kod zwraca poprawne wyniki. Zacznijmy zadanie, zajmując się odczytaniem danych z dokumentu. Skorzystamy w tym przypadku z with open(nazwa_pliku) as nazwa.

with open("pi.txt") as plik:
    linie = plik.readlines()
    for i in range(len(linie)):
        linie[i] = int(linie[i].rstrip())

with open("pi.txt") as plik:

linie = plik.readlines()

for i in range(len(linie)):

linie[i] = int(linie[i].rstrip())

Otwieramy plik i tworzymy listę, gdzie każdy element to kolejny wiersz pliku pi.txt. Następnie usuwamy białe znaki (spacje, entery itp) z końca każdej linii i konwertujemy go na liczbę (domyślnie python zapisuje jako tekst).

fragmentyDwucyfrowe = []
for i in range(len(linie)-1):
    fragmentyDwucyfrowe.append(str(linie[i]) + str(linie[i+1]))

fragmentyDwucyfrowe = []

for i in range(len(linie)-1):

fragmentyDwucyfrowe.append(str(linie[i]) + str(linie[i+1]))

W podpunktach 3.1 i 3.2 mamy do czynienia z “fragmentami dwucyfrowymi” dlatego warto stworzyć listę, która ułatwi działania na nich. Teraz zamiast na nowo konstruować je za każdym razem, możemy po prostu użyć konkretnego elementu tej listy.

licznik = 0
for fragment in fragmentyDwucyfrowe:
    if int(fragment) > 90:
        licznik += 1
print(licznik)

licznik = 0

for fragment in fragmentyDwucyfrowe:

if int(fragment) > 90:

licznik += 1

print(licznik)

Implementacja – C++

Biblioteki:

#include <iostream>
#include <fstream>
#include <string>

#include <iostream>

#include <fstream>

#include <string>

Kod główny:

const int MAX_LINES = 10000; // Maksymalna liczba linii

ifstream plik("pi.txt");
string linia;
int liczby[MAX_LINES];
int liczbaLinii = 0;

// Wczytywanie danych z pliku do tablicy
while (getline(plik, linia)) {
    istringstream iss(linia);
    iss >> liczby[liczbaLinii++];
}

// Tworzenie tablicy fragmentów dwucyfrowych poprzez łączenie kolejnych liczb w pary
string dwucyfroweFragmenty[MAX_LINES - 1];
for (int i = 0; i < liczbaLinii - 1; i++) {
    dwucyfroweFragmenty[i] = to_string(liczby[i]) + to_string(liczby[i + 1]);
}

int licznik = 0;
for (int i = 0; i < liczbaLinii - 1; i++) {
    if (stoi(dwucyfroweFragmenty[i]) > 90) {
        licznik++;
    }
}
cout << licznik << endl;

const int MAX_LINES = 10000; // Maksymalna liczba linii

ifstream plik("pi.txt");

string linia;

int liczby[MAX_LINES];

int liczbaLinii = 0;

// Wczytywanie danych z pliku do tablicy

while (getline(plik, linia)) {

istringstream iss(linia);

iss >> liczby[liczbaLinii++];

}

// Tworzenie tablicy fragmentów dwucyfrowych poprzez łączenie kolejnych liczb w pary

string dwucyfroweFragmenty[MAX_LINES - 1];

for (int i = 0; i < liczbaLinii - 1; i++) {

dwucyfroweFragmenty[i] = to_string(liczby[i]) + to_string(liczby[i + 1]);

}

int licznik = 0;

for (int i = 0; i < liczbaLinii - 1; i++) {

if (stoi(dwucyfroweFragmenty[i]) > 90) {

licznik++;

}

cout << licznik << endl;

Implementacja – Java

Biblioteki:

import java.io.BufferedReader;
import java.io.FileReader;
import java.io.IOException;

import java.io.BufferedReader;

import java.io.FileReader;

import java.io.IOException;

Kod główny:

try (BufferedReader br = new BufferedReader(new FileReader("pi.txt"))) {
    String linia;
    StringBuilder sb = new StringBuilder();
    while ((linia = br.readLine()) != null) { // Odczytanie linii z pliku
        sb.append(linia).append("\n"); // Dodanie odczytanej linii do StringBuildera
    }
    String[] linie = sb.toString().split("\n"); // Podział zawartości StringBuildera na tablicę linii
    int[] liczby = new int[linie.length];

    // Konwersja odczytanych linii na liczby całkowite i zapisanie ich do tablicy
    for (int i = 0; i < linie.length; i++) {
        liczby[i] = Integer.parseInt(linie[i].trim());
    }

    String[] dwucyfroweFragmenty = new String[liczby.length - 1]; // Inicjalizacja tablicy na dwucyfrowe fragmenty

    // Generowanie dwucyfrowych fragmentów i zapisanie ich do tablicy
    for (int i = 0; i < liczby.length - 1; i++) {
        dwucyfroweFragmenty[i] = Integer.toString(liczby[i]) + Integer.toString(liczby[i + 1]);
    }

    int licznik = 0;
    // Obliczanie liczby fragmentów większych od 90
    for (String fragment : dwucyfroweFragmenty) {
        if (Integer.parseInt(fragment) > 90) {
            licznik++;
        }
    }
    System.out.println(licznik);
}

try (BufferedReader br = new BufferedReader(new FileReader("pi.txt"))) {

String linia;

StringBuilder sb = new StringBuilder();

while ((linia = br.readLine()) != null) { // Odczytanie linii z pliku

sb.append(linia).append("\n"); // Dodanie odczytanej linii do StringBuildera

}

String[] linie = sb.toString().split("\n"); // Podział zawartości StringBuildera na tablicę linii

int[] liczby = new int[linie.length];

// Konwersja odczytanych linii na liczby całkowite i zapisanie ich do tablicy

for (int i = 0; i < linie.length; i++) {

liczby[i] = Integer.parseInt(linie[i].trim());

}

String[] dwucyfroweFragmenty = new String[liczby.length - 1]; // Inicjalizacja tablicy na dwucyfrowe fragmenty

// Generowanie dwucyfrowych fragmentów i zapisanie ich do tablicy

for (int i = 0; i < liczby.length - 1; i++) {

dwucyfroweFragmenty[i] = Integer.toString(liczby[i]) + Integer.toString(liczby[i + 1]);

}

int licznik = 0;

// Obliczanie liczby fragmentów większych od 90

for (String fragment : dwucyfroweFragmenty) {

if (Integer.parseInt(fragment) > 90) {

licznik++;

}

System.out.println(licznik);

}

Rozwiązanie:

902

Zadanie 3.2.

Do rozwiązania zadania najlepiej użyć słownika. Dla każdego fragmentu dwucyfrowego przypisze on liczbę jego wystąpień. Należy uzupełnić go wszystkimi stoma fragmentami, ponieważ gdybyśmy tworzyli słownik na podstawie fragmentów obecnych w pliku moglibyśmy jakieś pominąć, jeśli nie występowały ani razu, a o nich trzeba pamiętać jak pokazał plik przykładowy. Po stworzeniu słownika i wypełnieniu go sprytnie wykorzystując pętle, musimy utworzyć zmienne przechowujące fragmenty o minimalnej i maksymalnej liczbie wystąpień, a także liczbę ich wystąpień. Następnie klasycznie wyszukujemy minimalne i maksymalne wartości oraz zapisujemy je w zmiennych.

Pamiętaj, że zawsze w przypadku zadań “znajdź maksimum/minimum” najlepiej przypisać wartość pierwszego elementu. Dlaczego? Co w przypadku jeśli przypiszemy 0 jako wartość początkową minFragmentLiczba, a wśród fragmentów wszystkie będą występowały więcej razy? Wtedy nasz program zwróci 0 pomimo faktu, że to nie ono jest minimalną wartością. Alternatywą jest przypisanie bardzo małych lub dużych wartości min i maks np. maks = 9999999999999 i min = -9999999.

Po stworzeniu listy, rozwiązanie podpunktu 3.2 jest proste. Wystarczy zmienna, która będzie zliczała wystąpienia fragmentów większych od 90. Następnie za pomocą pętli sprawdzamy warunek dla każdego fragmentu i odpowiednio zwiększamy wartość zmiennej licznik. Na koniec wyświetlamy wartość licznika. Pamiętaj, że trzeba go skopiować i wkleić do pliku z odpowiedziami!

liczniki = {}
for i in range(10):
    for j in range(10):
        liczniki[str(i)+str(j)] = 0
  
for fragment in fragmentyDwucyfrowe:
    liczniki[fragment] += 1

minFragment = "00"
minFragmentLiczba = liczniki["00"]
maksFragment = "00"
maksFragmentLiczba = liczniki["00"]
for klucz in liczniki:
    if liczniki[klucz] < minFragmentLiczba:
        minFragment = klucz
        minFragmentLiczba = liczniki[klucz]
    if liczniki[klucz] > maksFragmentLiczba:
        maksFragment = klucz
        maksFragmentLiczba = liczniki[klucz]

liczniki = {}

for i in range(10):

for j in range(10):

liczniki[str(i)+str(j)] = 0

for fragment in fragmentyDwucyfrowe:

liczniki[fragment] += 1

minFragment = "00"

minFragmentLiczba = liczniki["00"]

maksFragment = "00"

maksFragmentLiczba = liczniki["00"]

for klucz in liczniki:

if liczniki[klucz] < minFragmentLiczba:

minFragment = klucz

minFragmentLiczba = liczniki[klucz]

if liczniki[klucz] > maksFragmentLiczba:

maksFragment = klucz

maksFragmentLiczba = liczniki[klucz]

Implementacja – C++

Biblioteki:

#include <iostream>
#include <string>

1 2	#include <iostream> #include <string>

Kod:

// Inicjalizacja dwuwymiarowej tablicy na liczniki fragmentów dwucyfrowych
int liczniki[10][10] = {0};

// Obliczanie wystąpień każdego dwucyfrowego fragmentu
for (int i = 0; i < liczbaLinii - 1; i++) {
    int x = dwucyfroweFragmenty[i][0] - '0'; // Pierwsza cyfra dwucyfrowego fragmentu
    int y = dwucyfroweFragmenty[i][1] - '0'; // Druga cyfra dwucyfrowego fragmentu
    liczniki[x][y]++; // Inkrementacja licznika dla odpowiedniego fragmentu
}

string minFragment = "00";
int minFragmentLiczba = liczniki[0][0];
string maksFragment = "00";
int maksFragmentLiczba = liczniki[0][0];

// Wyszukiwanie fragmentu o najmniejszej i największej liczbie wystąpień
for (int i = 0; i < 10; i++) {
    for (int j = 0; j < 10; j++) {
        if (liczniki[i][j] < minFragmentLiczba) {
            minFragment = to_string(i) + to_string(j);
            minFragmentLiczba = liczniki[i][j];
        }
        if (liczniki[i][j] > maksFragmentLiczba) {
            maksFragment = to_string(i) + to_string(j);
            maksFragmentLiczba = liczniki[i][j];
        }
    }
}

cout << minFragment << " " << minFragmentLiczba << endl;
cout << maksFragment << " " << maksFragmentLiczba << endl;

// Inicjalizacja dwuwymiarowej tablicy na liczniki fragmentów dwucyfrowych

int liczniki[10][10] = {0};

// Obliczanie wystąpień każdego dwucyfrowego fragmentu

for (int i = 0; i < liczbaLinii - 1; i++) {

int x = dwucyfroweFragmenty[i][0] - '0'; // Pierwsza cyfra dwucyfrowego fragmentu

int y = dwucyfroweFragmenty[i][1] - '0'; // Druga cyfra dwucyfrowego fragmentu

liczniki[x][y]++; // Inkrementacja licznika dla odpowiedniego fragmentu

}

string minFragment = "00";

int minFragmentLiczba = liczniki[0][0];

string maksFragment = "00";

int maksFragmentLiczba = liczniki[0][0];

// Wyszukiwanie fragmentu o najmniejszej i największej liczbie wystąpień

for (int i = 0; i < 10; i++) {

for (int j = 0; j < 10; j++) {

if (liczniki[i][j] < minFragmentLiczba) {

minFragment = to_string(i) + to_string(j);

minFragmentLiczba = liczniki[i][j];

}

if (liczniki[i][j] > maksFragmentLiczba) {

maksFragment = to_string(i) + to_string(j);

maksFragmentLiczba = liczniki[i][j];

}

cout << minFragment << " " << minFragmentLiczba << endl;

cout << maksFragment << " " << maksFragmentLiczba << endl;

Implementacja – Java

Biblioteki:

import java.util.Arrays;

1	import java.util.Arrays;

Kod:

int[][] liczniki = new int[10][10]; // Inicjalizacja dwuwymiarowej tablicy liczników

// Obliczanie wystąpień każdego dwucyfrowego fragmentu
for (int i = 0; i < liczby.length - 1; i++) {
    int x = dwucyfroweFragmenty[i].charAt(0) - '0'; // Pierwsza cyfra dwucyfrowego fragmentu
    int y = dwucyfroweFragmenty[i].charAt(1) - '0'; // Druga cyfra dwucyfrowego fragmentu
    liczniki[x][y]++; // Inkrementacja licznika dla odpowiedniego fragmentu
}

String minFragment = "00";
int minFragmentLiczba = liczniki[0][0];
String maksFragment = "00";
int maksFragmentLiczba = liczniki[0][0];

// Wyszukiwanie fragmentu o najmniejszej i największej liczbie wystąpień
for (int i = 0; i < 10; i++) {
    for (int j = 0; j < 10; j++) {
        if (liczniki[i][j] < minFragmentLiczba) {
            minFragment = Integer.toString(i) + Integer.toString(j);
            minFragmentLiczba = liczniki[i][j];
        }
        if (liczniki[i][j] > maksFragmentLiczba) {
            maksFragment = Integer.toString(i) + Integer.toString(j);
            maksFragmentLiczba = liczniki[i][j];
        }
    }
}

System.out.println(minFragment + " " + minFragmentLiczba);
System.out.println(maksFragment + " " + maksFragmentLiczba);

int[][] liczniki = new int[10][10]; // Inicjalizacja dwuwymiarowej tablicy liczników

// Obliczanie wystąpień każdego dwucyfrowego fragmentu

for (int i = 0; i < liczby.length - 1; i++) {

int x = dwucyfroweFragmenty[i].charAt(0) - '0'; // Pierwsza cyfra dwucyfrowego fragmentu

int y = dwucyfroweFragmenty[i].charAt(1) - '0'; // Druga cyfra dwucyfrowego fragmentu

liczniki[x][y]++; // Inkrementacja licznika dla odpowiedniego fragmentu

}

String minFragment = "00";

int minFragmentLiczba = liczniki[0][0];

String maksFragment = "00";

int maksFragmentLiczba = liczniki[0][0];

// Wyszukiwanie fragmentu o najmniejszej i największej liczbie wystąpień

for (int i = 0; i < 10; i++) {

for (int j = 0; j < 10; j++) {

if (liczniki[i][j] < minFragmentLiczba) {

minFragment = Integer.toString(i) + Integer.toString(j);

minFragmentLiczba = liczniki[i][j];

}

if (liczniki[i][j] > maksFragmentLiczba) {

maksFragment = Integer.toString(i) + Integer.toString(j);

maksFragmentLiczba = liczniki[i][j];

}

System.out.println(minFragment + " " + minFragmentLiczba);

System.out.println(maksFragment + " " + maksFragmentLiczba);

Rozwiązanie:

88 80

65 124

Zadanie 3.3.

Matura z informatyki 2023 - informacja do zadań 3.3 i 3.4 — Informacja do zadań 3.3. i 3.4.

W podpunkcie 3.3 oraz 3.4 mamy do czynienia z “ciągami rosnąco-malejącymi”, można się tym zająć na wiele sposobów np. generując listę wszystkich ciągów, a potem zliczać te które mają długość 6. Są sposoby szybsze i bardziej wydajne, ale na maturze nie liczy się nic oprócz wyniku końcowego. Można więc zrobić to w stylu “brute force”, czyli po prostu brać 6 kolejnych cyfr i sprawdzać czy tworzą one ciąg. Jest to rozwiązanie, które nie jest wydajne, ale jest najszybsze w napisaniu.

def czyRosnacy(ciag):
    for i in range(1,len(ciag)):
        if ciag[i-1] >= ciag[i]:
            return False
    return True
  
def czyMalejacy(ciag):
    for i in range(1,len(ciag)):
         if ciag[i-1] <= ciag[i]:
            return False
    return True


i = 0
licznik = 0
while i < len(linie)-6:
    lista = linie[i:i+6]
    for j in range(2,len(lista)-1):
        if czyRosnacy(lista[:j]) and czyMalejacy(lista[j:]):
            licznik += 1
            break
    i += 1
print(licznik)

def czyRosnacy(ciag):

for i in range(1,len(ciag)):

if ciag[i-1] >= ciag[i]:

return False

return True

def czyMalejacy(ciag):

for i in range(1,len(ciag)):

if ciag[i-1] <= ciag[i]:

return False

return True

i = 0

licznik = 0

while i < len(linie)-6:

lista = linie[i:i+6]

for j in range(2,len(lista)-1):

if czyRosnacy(lista[:j]) and czyMalejacy(lista[j:]):

licznik += 1

break

i += 1

print(licznik)

To rozwiązanie opiera się w dużej mierze na slicingu, warto zapoznać się z tym pojęciem przed maturą. Jego opis jest dostępny w artykule o przydatnych funkcjach w języku Python.

Jak widać sprawdzamy po prostu, czy pierwsze liczby tworzą ciąg rosnący, a pozostałe ciąg malejący, jeśli tak to zwiększamy licznik i przerywamy działanie pętli for używając break. Przerwanie jest bardzo ważne, bez niego moglibyśmy liczyć dany ciąg wielokrotnie.

Implementacja – C++

Biblioteki:

#include <iostream>

1	#include <iostream>

Funkcje:

bool czyRosnacy(int ciag[], int koniec) {
    // Funkcja sprawdzająca, czy ciąg liczb jest rosnący do określonego indeksu
    for (int i = 1; i < koniec; i++) {
        if (ciag[i - 1] >= ciag[i]) {
            return false;
        }
    }
    return true;
}

bool czyMalejacy(int ciag[], int start, int dlugosc) {
    // Funkcja sprawdzająca, czy ciąg liczb jest malejący od określonego indeksu do końca
    for (int i = start + 1; i < dlugosc; i++) {
        if (ciag[i - 1] <= ciag[i]) {
            return false;
        }
    }
    return true;
}

bool czyRosnacy(int ciag[], int koniec) {

// Funkcja sprawdzająca, czy ciąg liczb jest rosnący do określonego indeksu

for (int i = 1; i < koniec; i++) {

if (ciag[i - 1] >= ciag[i]) {

return false;

}

return true;

}

bool czyMalejacy(int ciag[], int start, int dlugosc) {

// Funkcja sprawdzająca, czy ciąg liczb jest malejący od określonego indeksu do końca

for (int i = start + 1; i < dlugosc; i++) {

if (ciag[i - 1] <= ciag[i]) {

return false;

}

return true;

}

Kod główny:

int indeks = 0;
licznik = 0;

// Sprawdzanie sekwencji rosnących i malejących liczb
while (indeks < liczbaLinii - 6) {
    int lista[6];
    copy(liczby + indeks, liczby + indeks + 6, lista);
    for (int j = 2; j < 5; j++) {
        if (czyRosnacy(lista, j) && czyMalejacy(lista, j, 6)) {
            licznik++;
            break;
        }
    }
    indeks++;
}

cout << licznik << endl;

int indeks = 0;

licznik = 0;

// Sprawdzanie sekwencji rosnących i malejących liczb

while (indeks < liczbaLinii - 6) {

int lista[6];

copy(liczby + indeks, liczby + indeks + 6, lista);

for (int j = 2; j < 5; j++) {

if (czyRosnacy(lista, j) && czyMalejacy(lista, j, 6)) {

licznik++;

break;

}

indeks++;

}

cout << licznik << endl;

Implementacja – Java

Funkcje:

// Sprawdzanie, czy ciąg liczb jest rosnący do określonego indeksu
static boolean czyRosnacy(int[] ciag, int koniec) {
    for (int i = 1; i < koniec; i++) {
        if (ciag[i - 1] >= ciag[i]) {
            return false;
        }
    }
    return true;
}

// Sprawdzanie, czy ciąg liczb jest malejący od określonego indeksu
static boolean czyMalejacy(int[] ciag, int start) {
    for (int i = start + 1; i < ciag.length; i++) {
        if (ciag[i - 1] <= ciag[i]) {
            return false;
        }
    }
    return true;
}

// Sprawdzanie, czy ciąg liczb jest rosnący do określonego indeksu

static boolean czyRosnacy(int[] ciag, int koniec) {

for (int i = 1; i < koniec; i++) {

if (ciag[i - 1] >= ciag[i]) {

return false;

}

return true;

}

// Sprawdzanie, czy ciąg liczb jest malejący od określonego indeksu

static boolean czyMalejacy(int[] ciag, int start) {

for (int i = start + 1; i < ciag.length; i++) {

if (ciag[i - 1] <= ciag[i]) {

return false;

}

return true;

}

Kod główny:

int indeks = 0;
licznik = 0;

// Sprawdzanie sekwencji rosnących i malejących liczb
while (indeks < liczby.length - 6) {
    int[] lista = new int[6];
    System.arraycopy(liczby, indeks, lista, 0, 6);
    for (int j = 2; j < lista.length - 1; j++) {
        if (czyRosnacy(lista, j) && czyMalejacy(lista, j)) {
            licznik++;
            break;
        }
    }
    indeks++;
}
System.out.println(licznik);

int indeks = 0;

licznik = 0;

// Sprawdzanie sekwencji rosnących i malejących liczb

while (indeks < liczby.length - 6) {

int[] lista = new int[6];

System.arraycopy(liczby, indeks, lista, 0, 6);

for (int j = 2; j < lista.length - 1; j++) {

if (czyRosnacy(lista, j) && czyMalejacy(lista, j)) {

licznik++;

break;

}

indeks++;

}

System.out.println(licznik);

Rozwiązanie:

214

Zadanie 3.4.

licznik = 1
dlugosc = 6
maksIndeks = 0
while licznik > 0:
    i = 0
    licznik = 0
    while i < len(linie)-dlugosc:
        lista = linie[i:i+dlugosc]
        for j in range(2,len(lista)-1):
            if czyRosnacy(lista[:j]) and czyMalejacy(lista[j:]):
                licznik += 1
                maksIndeks = i
                break
            i += 1
    dlugosc += 1
print(maksIndeks+1," ",*linie[maksIndeks:maksIndeks+dlugosc-1],sep="")

licznik = 1

dlugosc = 6

maksIndeks = 0

while licznik > 0:

i = 0

licznik = 0

while i < len(linie)-dlugosc:

lista = linie[i:i+dlugosc]

for j in range(2,len(lista)-1):

if czyRosnacy(lista[:j]) and czyMalejacy(lista[j:]):

licznik += 1

maksIndeks = i

break

i += 1

dlugosc += 1

print(maksIndeks+1," ",*linie[maksIndeks:maksIndeks+dlugosc-1],sep="")

Do podpunktu 3.4 możemy wykorzystać kod z podpunktu 3.3. Najlepiej jest go po prostu skopiować i zmienić ustaloną z góry długość 6 na zmienną dlugosc, która będzie się zwiększała.

Zaczynamy od długości 6, ponieważ wiemy, że tej długości ciągi na pewno są w pliku. Następnie zwiększamy dlugosc i liczymy liczbę wystąpień tego odcinka. Za każdym razem sprawdzamy, czy występuje ich więcej niż zero, gdy okaże się, że ciągi danej długości nie występują to znaczy, że poprzednia długość była tą największą. Zauważ, że zapamiętujemy indeks ostatnio znalezionego ciągu, ponieważ najdłuższy ciąg jest ostatnim, który znajdziemy tym sposobem. Wystarczy wyświetlić wartość tej zmiennej w odpowiedzi +1, ponieważ indeksy w pliku są indeksowane od 1, a na naszej liście od 0.

Przy wypisywaniu z pomocą print używamy * żeby “przekazać” wszystkie elementy listy jako jej argumenty. Żeby wyświetlić tylko konkretny fragment listy znowu używamy slicingu. Wyświetlamy wszystkie elementy odległe od maksIndeks o maksymalną długość. Maksymalna długość jest o 1 mniejsza od dlugosc, ponieważ zmienna na koniec ma wartość pierwszej długości, w której nie ma żadnych ciągów. Tutaj rodzi się pytanie, co jeśli na przykład nie ma ciągów o długości 10, ale o długości 11 już są? Czy wtedy program zwraca zły wynik? Na szczęście do takiej sytuacji nigdy nie dojdzie, ponieważ zbiory mniejszej długości są podciągami tych dłuższych tzn. jeśli istnieje ciąg o długości 11 to istnieje też ciąg o długości 10.

Implementacja – C++

Biblioteki:

#include <iostream>

1	#include <iostream>

Funkcje:

bool czyRosnacy(int ciag[], int koniec) {
    // Funkcja sprawdzająca, czy ciąg liczb jest rosnący do określonego indeksu
    for (int i = 1; i < koniec; i++) {
        if (ciag[i - 1] >= ciag[i]) {
            return false;
        }
    }
    return true;
}

bool czyMalejacy(int ciag[], int start, int dlugosc) {
    // Funkcja sprawdzająca, czy ciąg liczb jest malejący od określonego indeksu do końca
    for (int i = start + 1; i < dlugosc; i++) {
        if (ciag[i - 1] <= ciag[i]) {
            return false;
        }
    }
    return true;
}

bool czyRosnacy(int ciag[], int koniec) {

// Funkcja sprawdzająca, czy ciąg liczb jest rosnący do określonego indeksu

for (int i = 1; i < koniec; i++) {

if (ciag[i - 1] >= ciag[i]) {

return false;

}

return true;

}

bool czyMalejacy(int ciag[], int start, int dlugosc) {

// Funkcja sprawdzająca, czy ciąg liczb jest malejący od określonego indeksu do końca

for (int i = start + 1; i < dlugosc; i++) {

if (ciag[i - 1] <= ciag[i]) {

return false;

}

return true;

}

Kod główny:

int dlugosc = 6;
int maksIndeks = 0;

// Wyszukiwanie najdłuższej sekwencji rosnącej i malejącej
while (licznik > 0) {
    indeks = 0;
    licznik = 0;
    while (indeks < liczbaLinii - dlugosc) {
        int lista[dlugosc];
        copy(liczby + indeks, liczby + indeks + dlugosc, lista);
        for (int j = 2; j < dlugosc - 1; j++) {
            if (czyRosnacy(lista, j) && czyMalejacy(lista, j, dlugosc)) {
                licznik++;
                maksIndeks = indeks;
                break;
            }
        }
        indeks++;
    }
    dlugosc++;
}

cout << maksIndeks + 1 << endl;

// Wyświetlanie najdłuższej sekwencji
for (int i = maksIndeks; i < maksIndeks + dlugosc - 2; i++) {
    cout << liczby[i];
}

int dlugosc = 6;

int maksIndeks = 0;

// Wyszukiwanie najdłuższej sekwencji rosnącej i malejącej

while (licznik > 0) {

indeks = 0;

licznik = 0;

while (indeks < liczbaLinii - dlugosc) {

int lista[dlugosc];

copy(liczby + indeks, liczby + indeks + dlugosc, lista);

for (int j = 2; j < dlugosc - 1; j++) {

if (czyRosnacy(lista, j) && czyMalejacy(lista, j, dlugosc)) {

licznik++;

maksIndeks = indeks;

break;

}

indeks++;

}

dlugosc++;

}

cout << maksIndeks + 1 << endl;

// Wyświetlanie najdłuższej sekwencji

for (int i = maksIndeks; i < maksIndeks + dlugosc - 2; i++) {

cout << liczby[i];

}

Implementacja – Java

Funkcje:

// Sprawdzanie, czy ciąg liczb jest rosnący do określonego indeksu
static boolean czyRosnacy(int[] ciag, int koniec) {
    for (int i = 1; i < koniec; i++) {
        if (ciag[i - 1] >= ciag[i]) {
            return false;
        }
    }
    return true;
}

// Sprawdzanie, czy ciąg liczb jest malejący od określonego indeksu
static boolean czyMalejacy(int[] ciag, int start) {
    for (int i = start + 1; i < ciag.length; i++) {
        if (ciag[i - 1] <= ciag[i]) {
            return false;
        }
    }
}

// Sprawdzanie, czy ciąg liczb jest rosnący do określonego indeksu

static boolean czyRosnacy(int[] ciag, int koniec) {

for (int i = 1; i < koniec; i++) {

if (ciag[i - 1] >= ciag[i]) {

return false;

}

return true;

}

// Sprawdzanie, czy ciąg liczb jest malejący od określonego indeksu

static boolean czyMalejacy(int[] ciag, int start) {

for (int i = start + 1; i < ciag.length; i++) {

if (ciag[i - 1] <= ciag[i]) {

return false;

}

Kod główny:

int dlugosc = 6;
int maksIndeks = 0;

// Wyszukiwanie najdłuższej sekwencji rosnącej i malejącej
while (licznik > 0) {
    indeks = 0;
    licznik = 0;
    while (indeks < liczby.length - dlugosc) {
        int[] lista = new int[dlugosc];
        System.arraycopy(liczby, indeks, lista, 0, dlugosc);
        for (int j = 2; j < dlugosc - 1; j++) {
            if (czyRosnacy(lista, j) && czyMalejacy(lista, j)) {
                licznik++;
                maksIndeks = indeks;
                break;
            }
        }
        indeks++;
    }
    dlugosc++;
}
System.out.println((maksIndeks + 1) + " ");

// Wyświetlanie najdłuższej sekwencji
for (int i = maksIndeks; i < maksIndeks + dlugosc - 2; i++) {
    System.out.print(liczby[i]);
}

int dlugosc = 6;

int maksIndeks = 0;

// Wyszukiwanie najdłuższej sekwencji rosnącej i malejącej

while (licznik > 0) {

indeks = 0;

licznik = 0;

while (indeks < liczby.length - dlugosc) {

int[] lista = new int[dlugosc];

System.arraycopy(liczby, indeks, lista, 0, dlugosc);

for (int j = 2; j < dlugosc - 1; j++) {

if (czyRosnacy(lista, j) && czyMalejacy(lista, j)) {

licznik++;

maksIndeks = indeks;

break;

}

indeks++;

}

dlugosc++;

}

System.out.println((maksIndeks + 1) + " ");

// Wyświetlanie najdłuższej sekwencji

for (int i = maksIndeks; i < maksIndeks + dlugosc - 2; i++) {

System.out.print(liczby[i]);

}

Rozwiązanie:

2781

014576540

Pełny kod 3.1-3.4 – implementacja w python, C++ i java

Implementacja – Python

# Otwarcie pliku "pi.txt" i odczytanie wszystkich linii
with open("pi.txt") as plik:
    linie = plik.readlines()

# Konwersja odczytanych linii na liczby całkowite i usunięcie białych znaków z końca każdej linii
    for i in range(len(linie)): 
        linie[i] = int(linie[i].rstrip())

# Tworzenie listy fragmentów dwucyfrowych poprzez łączenie kolejnych liczb w pary
fragmentyDwucyfrowe = []
for i in range(len(linie)-1):
    fragmentyDwucyfrowe.append(str(linie[i]) + str(linie[i+1]))

# Liczenie fragmentów dwucyfrowych większych niż 90
licznik = 0
for fragment in fragmentyDwucyfrowe:
    if int(fragment) > 90:
        licznik += 1
print(licznik)

# Inicjalizacja słownika liczników dla wszystkich możliwych par dwucyfrowych liczb
liczniki = {}
for i in range(10):
    for j in range(10):
        liczniki[str(i)+str(j)] = 0

# Zliczanie wystąpień poszczególnych fragmentów dwucyfrowych
for fragment in fragmentyDwucyfrowe:
    liczniki[fragment] += 1


# Inicjalizacja zmiennych przechowujących informacje o najmniejszym i największym fragmencie oraz ich liczbie wystąpień
minFragment = "00"
minFragmentLiczba = liczniki["00"]
maksFragment = "00"
maksFragmentLiczba = liczniki["00"]

# Znalezienie najmniejszego i największego fragmentu oraz ich liczby wystąpień
for klucz in liczniki:
    if liczniki[klucz] < minFragmentLiczba:
        minFragment = klucz
        minFragmentLiczba = liczniki[klucz]
    if liczniki[klucz] > maksFragmentLiczba:
        maksFragment = klucz
        maksFragmentLiczba = liczniki[klucz]

print(minFragment, minFragmentLiczba)
print(maksFragment, maksFragmentLiczba)

# Funkcja sprawdzająca, czy ciąg jest rosnący
def czyRosnacy(ciag):
    for i in range(1,len(ciag)):
        if ciag[i-1] >= ciag[i]:
            return False
    return True
 
# Funkcja sprawdzająca, czy ciąg jest malejący
def czyMalejacy(ciag):
    for i in range(1,len(ciag)):
        if ciag[i-1] <= ciag[i]:
            return False
    return True

# Przeszukiwanie linii w poszukiwaniu fragmentów spełniających warunki
i = 0
licznik = 0
while i < len(linie)-6:
    lista = linie[i:i+6]
    for j in range(2,len(lista)-1):
        if czyRosnacy(lista[:j]) and czyMalejacy(lista[j:]):
            licznik += 1
            break
    i += 1
print(licznik)

# Wyszukiwanie najdłuższego fragmentu spełniającego warunki i jego indeksu początkowego
licznik = 1
dlugosc = 6
maksIndeks = 0
while licznik > 0:
    i = 0
    licznik = 0
    while i < len(linie)-dlugosc:
        lista = linie[i:i+dlugosc]
        for j in range(2,len(lista)-1):
            if czyRosnacy(lista[:j]) and czyMalejacy(lista[j:]):
                licznik += 1
                maksIndeks = i
                break
        i += 1
    dlugosc += 1
print(maksIndeks+1)
print(*linie[maksIndeks:maksIndeks+dlugosc-2],sep="")

# Otwarcie pliku "pi.txt" i odczytanie wszystkich linii

with open("pi.txt") as plik:

linie = plik.readlines()

# Konwersja odczytanych linii na liczby całkowite i usunięcie białych znaków z końca każdej linii

for i in range(len(linie)):

linie[i] = int(linie[i].rstrip())

# Tworzenie listy fragmentów dwucyfrowych poprzez łączenie kolejnych liczb w pary

fragmentyDwucyfrowe = []

for i in range(len(linie)-1):

fragmentyDwucyfrowe.append(str(linie[i]) + str(linie[i+1]))

# Liczenie fragmentów dwucyfrowych większych niż 90

licznik = 0

for fragment in fragmentyDwucyfrowe:

if int(fragment) > 90:

licznik += 1

print(licznik)

# Inicjalizacja słownika liczników dla wszystkich możliwych par dwucyfrowych liczb

liczniki = {}

for i in range(10):

for j in range(10):

liczniki[str(i)+str(j)] = 0

# Zliczanie wystąpień poszczególnych fragmentów dwucyfrowych

for fragment in fragmentyDwucyfrowe:

liczniki[fragment] += 1

# Inicjalizacja zmiennych przechowujących informacje o najmniejszym i największym fragmencie oraz ich liczbie wystąpień

minFragment = "00"

minFragmentLiczba = liczniki["00"]

maksFragment = "00"

maksFragmentLiczba = liczniki["00"]

# Znalezienie najmniejszego i największego fragmentu oraz ich liczby wystąpień

for klucz in liczniki:

if liczniki[klucz] < minFragmentLiczba:

minFragment = klucz

minFragmentLiczba = liczniki[klucz]

if liczniki[klucz] > maksFragmentLiczba:

maksFragment = klucz

maksFragmentLiczba = liczniki[klucz]

print(minFragment, minFragmentLiczba)

print(maksFragment, maksFragmentLiczba)

# Funkcja sprawdzająca, czy ciąg jest rosnący

def czyRosnacy(ciag):

for i in range(1,len(ciag)):

if ciag[i-1] >= ciag[i]:

return False

return True

# Funkcja sprawdzająca, czy ciąg jest malejący

def czyMalejacy(ciag):

for i in range(1,len(ciag)):

if ciag[i-1] <= ciag[i]:

return False

return True

# Przeszukiwanie linii w poszukiwaniu fragmentów spełniających warunki

i = 0

licznik = 0

while i < len(linie)-6:

lista = linie[i:i+6]

for j in range(2,len(lista)-1):

if czyRosnacy(lista[:j]) and czyMalejacy(lista[j:]):

licznik += 1

break

i += 1

print(licznik)

# Wyszukiwanie najdłuższego fragmentu spełniającego warunki i jego indeksu początkowego

licznik = 1

dlugosc = 6

maksIndeks = 0

while licznik > 0:

i = 0

licznik = 0

while i < len(linie)-dlugosc:

lista = linie[i:i+dlugosc]

for j in range(2,len(lista)-1):

if czyRosnacy(lista[:j]) and czyMalejacy(lista[j:]):

licznik += 1

maksIndeks = i

break

i += 1

dlugosc += 1

print(maksIndeks+1)

print(*linie[maksIndeks:maksIndeks+dlugosc-2],sep="")

Implementacja – C++

#include <iostream>
#include <fstream>
#include <sstream>

using namespace std;

const int MAX_LINES = 10000; // Maksymalna liczba linii

bool czyRosnacy(int ciag[], int koniec) {
    // Funkcja sprawdzająca, czy ciąg liczb jest rosnący do określonego indeksu
    for (int i = 1; i < koniec; i++) {
        if (ciag[i - 1] >= ciag[i]) {
            return false;
        }
    }
    return true;
}

bool czyMalejacy(int ciag[], int start, int dlugosc) {
    // Funkcja sprawdzająca, czy ciąg liczb jest malejący od określonego indeksu do końca
    for (int i = start + 1; i < dlugosc; i++) {
        if (ciag[i - 1] <= ciag[i]) {
            return false;
        }
    }
    return true;
}


int main() {
    ifstream plik("pi.txt"); // Otwarcie pliku do odczytu
    string linia;
    int liczby[MAX_LINES]; // Tablica na liczby
    int liczbaLinii = 0;

    // Wczytywanie danych z pliku do tablicy
    while (getline(plik, linia) && liczbaLinii < MAX_LINES) {
        istringstream iss(linia);
        iss >> liczby[liczbaLinii++];
    }

    // Tworzenie tablicy fragmentów dwucyfrowych poprzez łączenie kolejnych liczb w pary
    string dwucyfroweFragmenty[MAX_LINES - 1];
    for (int i = 0; i < liczbaLinii - 1; i++) {
        dwucyfroweFragmenty[i] = to_string(liczby[i]) + to_string(liczby[i + 1]);
    }

    int licznik = 0;
    // Obliczanie liczby fragmentów większych od 90
    for (int i = 0; i < liczbaLinii - 1; i++) {
        if (stoi(dwucyfroweFragmenty[i]) > 90) {
            licznik++;
        }
    }
    cout << licznik << endl;

    // Inicjalizacja dwuwymiarowej tablicy na liczniki fragmentów dwucyfrowych
    int liczniki[10][10] = {0};

    // Obliczanie wystąpień każdego dwucyfrowego fragmentu
    for (int i = 0; i < liczbaLinii - 1; i++) {
        int x = dwucyfroweFragmenty[i][0] - '0'; // Pierwsza cyfra dwucyfrowego fragmentu
        int y = dwucyfroweFragmenty[i][1] - '0'; // Druga cyfra dwucyfrowego fragmentu
        liczniki[x][y]++; // Inkrementacja licznika dla odpowiedniego fragmentu
    }

    string minFragment = "00";
    int minFragmentLiczba = liczniki[0][0];
    string maksFragment = "00";
    int maksFragmentLiczba = liczniki[0][0];

    // Wyszukiwanie fragmentu o najmniejszej i największej liczbie wystąpień
    for (int i = 0; i < 10; i++) {
        for (int j = 0; j < 10; j++) {
            if (liczniki[i][j] < minFragmentLiczba) {
                minFragment = to_string(i) + to_string(j);
                minFragmentLiczba = liczniki[i][j];
            }
            if (liczniki[i][j] > maksFragmentLiczba) {
                maksFragment = to_string(i) + to_string(j);
                maksFragmentLiczba = liczniki[i][j];
            }
        }
    }

    cout << minFragment << " " << minFragmentLiczba << endl;
    cout << maksFragment << " " << maksFragmentLiczba << endl;

    int indeks = 0;
    licznik = 0;

    // Sprawdzanie sekwencji rosnących i malejących liczb
    while (indeks < liczbaLinii - 6) {
        int lista[6];
        copy(liczby + indeks, liczby + indeks + 6, lista);
        for (int j = 2; j < 5; j++) {
            if (czyRosnacy(lista, j) && czyMalejacy(lista, j, 6)) {
                licznik++;
                break;
                }
        }
        indeks++;
    }

    cout << licznik << endl;

    int dlugosc = 6;
    int maksIndeks = 0;

    // Wyszukiwanie najdłuższej sekwencji rosnącej i malejącej
    while (licznik > 0) {
        indeks = 0;
        licznik = 0;
        while (indeks < liczbaLinii - dlugosc) {
            int lista[dlugosc];
            copy(liczby + indeks, liczby + indeks + dlugosc, lista);
            for (int j = 2; j < dlugosc - 1; j++) {
                if (czyRosnacy(lista, j) && czyMalejacy(lista, j, dlugosc)) {
                    licznik++;
                    maksIndeks = indeks;
                    break;
                }
            }
            indeks++;
        }
        dlugosc++;
    }

    cout << maksIndeks + 1 << endl;

    // Wyświetlanie najdłuższej sekwencji
    for (int i = maksIndeks; i < maksIndeks + dlugosc - 2; i++) {
        cout << liczby[i];
    }

    return 0;
}

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

#include <iostream>

#include <fstream>

#include <sstream>

using namespace std;

const int MAX_LINES = 10000; // Maksymalna liczba linii

bool czyRosnacy(int ciag[], int koniec) {

// Funkcja sprawdzająca, czy ciąg liczb jest rosnący do określonego indeksu

for (int i = 1; i < koniec; i++) {

if (ciag[i - 1] >= ciag[i]) {

return false;

}

return true;

}

bool czyMalejacy(int ciag[], int start, int dlugosc) {

// Funkcja sprawdzająca, czy ciąg liczb jest malejący od określonego indeksu do końca

for (int i = start + 1; i < dlugosc; i++) {

if (ciag[i - 1] <= ciag[i]) {

return false;

}

return true;

}

int main() {

ifstream plik("pi.txt"); // Otwarcie pliku do odczytu

string linia;

int liczby[MAX_LINES]; // Tablica na liczby

int liczbaLinii = 0;

// Wczytywanie danych z pliku do tablicy

while (getline(plik, linia) && liczbaLinii < MAX_LINES) {

istringstream iss(linia);

iss >> liczby[liczbaLinii++];

}

// Tworzenie tablicy fragmentów dwucyfrowych poprzez łączenie kolejnych liczb w pary

string dwucyfroweFragmenty[MAX_LINES - 1];

for (int i = 0; i < liczbaLinii - 1; i++) {

dwucyfroweFragmenty[i] = to_string(liczby[i]) + to_string(liczby[i + 1]);

}

int licznik = 0;

// Obliczanie liczby fragmentów większych od 90

for (int i = 0; i < liczbaLinii - 1; i++) {

if (stoi(dwucyfroweFragmenty[i]) > 90) {

licznik++;

}

cout << licznik << endl;

// Inicjalizacja dwuwymiarowej tablicy na liczniki fragmentów dwucyfrowych

int liczniki[10][10] = {0};

// Obliczanie wystąpień każdego dwucyfrowego fragmentu

for (int i = 0; i < liczbaLinii - 1; i++) {

int x = dwucyfroweFragmenty[i][0] - '0'; // Pierwsza cyfra dwucyfrowego fragmentu

int y = dwucyfroweFragmenty[i][1] - '0'; // Druga cyfra dwucyfrowego fragmentu

liczniki[x][y]++; // Inkrementacja licznika dla odpowiedniego fragmentu

}

string minFragment = "00";

int minFragmentLiczba = liczniki[0][0];

string maksFragment = "00";

int maksFragmentLiczba = liczniki[0][0];

// Wyszukiwanie fragmentu o najmniejszej i największej liczbie wystąpień

for (int i = 0; i < 10; i++) {

for (int j = 0; j < 10; j++) {

if (liczniki[i][j] < minFragmentLiczba) {

minFragment = to_string(i) + to_string(j);

minFragmentLiczba = liczniki[i][j];

}

if (liczniki[i][j] > maksFragmentLiczba) {

maksFragment = to_string(i) + to_string(j);

maksFragmentLiczba = liczniki[i][j];

}

cout << minFragment << " " << minFragmentLiczba << endl;

cout << maksFragment << " " << maksFragmentLiczba << endl;

int indeks = 0;

licznik = 0;

// Sprawdzanie sekwencji rosnących i malejących liczb

while (indeks < liczbaLinii - 6) {

int lista[6];

copy(liczby + indeks, liczby + indeks + 6, lista);

for (int j = 2; j < 5; j++) {

if (czyRosnacy(lista, j) && czyMalejacy(lista, j, 6)) {

licznik++;

break;

}

indeks++;

}

cout << licznik << endl;

int dlugosc = 6;

int maksIndeks = 0;

// Wyszukiwanie najdłuższej sekwencji rosnącej i malejącej

while (licznik > 0) {

indeks = 0;

licznik = 0;

while (indeks < liczbaLinii - dlugosc) {

int lista[dlugosc];

copy(liczby + indeks, liczby + indeks + dlugosc, lista);

for (int j = 2; j < dlugosc - 1; j++) {

if (czyRosnacy(lista, j) && czyMalejacy(lista, j, dlugosc)) {

licznik++;

maksIndeks = indeks;

break;

}

indeks++;

}

dlugosc++;

}

cout << maksIndeks + 1 << endl;

// Wyświetlanie najdłuższej sekwencji

for (int i = maksIndeks; i < maksIndeks + dlugosc - 2; i++) {

cout << liczby[i];

}

return 0;

}

Implementacja – Java

import java.io.BufferedReader;
import java.io.FileReader;
import java.io.IOException;

public class Main {
    public static void main(String[] args) {
        try (BufferedReader br = new BufferedReader(new FileReader("pi.txt"))) { // Otwarcie pliku do odczytu
            String linia;
            StringBuilder sb = new StringBuilder();
            while ((linia = br.readLine()) != null) { // Odczytanie linii z pliku
                sb.append(linia).append("\n"); // Dodanie odczytanej linii do StringBuildera
            }
            String[] linie = sb.toString().split("\n"); // Podział zawartości StringBuildera na tablicę linii
            int[] liczby = new int[linie.length]; // Inicjalizacja tablicy na liczby

            // Konwersja odczytanych linii na liczby całkowite i zapisanie ich do tablicy
            for (int i = 0; i < linie.length; i++) {
                liczby[i] = Integer.parseInt(linie[i].trim());
            }

            String[] dwucyfroweFragmenty = new String[liczby.length - 1]; // Inicjalizacja tablicy na dwucyfrowe fragmenty

            // Generowanie dwucyfrowych fragmentów i zapisanie ich do tablicy
            for (int i = 0; i < liczby.length - 1; i++) {
                dwucyfroweFragmenty[i] = Integer.toString(liczby[i]) + Integer.toString(liczby[i + 1]);
            }

            int licznik = 0;
            // Obliczanie liczby fragmentów większych od 90
            for (String fragment : dwucyfroweFragmenty) {
                if (Integer.parseInt(fragment) > 90) {
                    licznik++;
                }
            }
            System.out.println(licznik);

            int[][] liczniki = new int[10][10]; // Inicjalizacja dwuwymiarowej tablicy liczników

            // Obliczanie wystąpień każdego dwucyfrowego fragmentu
            for (int i = 0; i < liczby.length - 1; i++) {
                int x = dwucyfroweFragmenty[i].charAt(0) - '0'; // Pierwsza cyfra dwucyfrowego fragmentu
                int y = dwucyfroweFragmenty[i].charAt(1) - '0'; // Druga cyfra dwucyfrowego fragmentu
                liczniki[x][y]++; // Inkrementacja licznika dla odpowiedniego fragmentu
            }

            String minFragment = "00";
            int minFragmentLiczba = liczniki[0][0];
            String maksFragment = "00";
            int maksFragmentLiczba = liczniki[0][0];

            // Wyszukiwanie fragmentu o najmniejszej i największej liczbie wystąpień
            for (int i = 0; i < 10; i++) {
                for (int j = 0; j < 10; j++) {
                    if (liczniki[i][j] < minFragmentLiczba) {
                        minFragment = Integer.toString(i) + Integer.toString(j);
                        minFragmentLiczba = liczniki[i][j];
                    }
                    if (liczniki[i][j] > maksFragmentLiczba) {
                        maksFragment = Integer.toString(i) + Integer.toString(j);
                        maksFragmentLiczba = liczniki[i][j];
                    }
                }
            }

            System.out.println(minFragment + " " + minFragmentLiczba);
            System.out.println(maksFragment + " " + maksFragmentLiczba);

            int indeks = 0;
            licznik = 0;

            // Sprawdzanie sekwencji rosnących i malejących liczb
            while (indeks < liczby.length - 6) {
                int[] lista = new int[6];
                System.arraycopy(liczby, indeks, lista, 0, 6);
                for (int j = 2; j < lista.length - 1; j++) {
                    if (czyRosnacy(lista, j) && czyMalejacy(lista, j)) {
                        licznik++;
                        break;
                    }
                }
                indeks++;
            }
            System.out.println(licznik);

            int dlugosc = 6;
            int maksIndeks = 0;

            // Wyszukiwanie najdłuższej sekwencji rosnącej i malejącej
            while (licznik > 0) {
                indeks = 0;
                licznik = 0;
                while (indeks < liczby.length - dlugosc) {
                    int[] lista = new int[dlugosc];
                    System.arraycopy(liczby, indeks, lista, 0, dlugosc);
                    for (int j = 2; j < dlugosc - 1; j++) {
                        if (czyRosnacy(lista, j) && czyMalejacy(lista, j)) {
                            licznik++;
                            maksIndeks = indeks;
                            break;
                        }
                    }
                    indeks++;
                }
                dlugosc++;
            }
            System.out.println((maksIndeks + 1) + " ");

            // Wyświetlanie najdłuższej sekwencji
            for (int i = maksIndeks; i < maksIndeks + dlugosc - 2; i++) {
                System.out.print(liczby[i]);
            }
        } catch (IOException e) {
            e.printStackTrace(); // Wyświetlenie informacji o błędzie wejścia/wyjścia
        }
    }

    // Sprawdzanie, czy ciąg liczb jest rosnący do określonego indeksu
    static boolean czyRosnacy(int[] ciag, int koniec) {
        for (int i = 1; i < koniec; i++) {
            if (ciag[i - 1] >= ciag[i]) {
                return false;
            }
        }
        return true;
    }

    // Sprawdzanie, czy ciąg liczb jest malejący od określonego indeksu
    static boolean czyMalejacy(int[] ciag, int start) {
        for (int i = start + 1; i < ciag.length; i++) {
            if (ciag[i - 1] <= ciag[i]) {
                return false;
            }
        }
        return true;
    }
}

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

import java.io.BufferedReader;

import java.io.FileReader;

import java.io.IOException;

public class Main {

public static void main(String[] args) {

try (BufferedReader br = new BufferedReader(new FileReader("pi.txt"))) { // Otwarcie pliku do odczytu

String linia;

StringBuilder sb = new StringBuilder();

while ((linia = br.readLine()) != null) { // Odczytanie linii z pliku

sb.append(linia).append("\n"); // Dodanie odczytanej linii do StringBuildera

}

String[] linie = sb.toString().split("\n"); // Podział zawartości StringBuildera na tablicę linii

int[] liczby = new int[linie.length]; // Inicjalizacja tablicy na liczby

// Konwersja odczytanych linii na liczby całkowite i zapisanie ich do tablicy

for (int i = 0; i < linie.length; i++) {

liczby[i] = Integer.parseInt(linie[i].trim());

}

String[] dwucyfroweFragmenty = new String[liczby.length - 1]; // Inicjalizacja tablicy na dwucyfrowe fragmenty

// Generowanie dwucyfrowych fragmentów i zapisanie ich do tablicy

for (int i = 0; i < liczby.length - 1; i++) {

dwucyfroweFragmenty[i] = Integer.toString(liczby[i]) + Integer.toString(liczby[i + 1]);

}

int licznik = 0;

// Obliczanie liczby fragmentów większych od 90

for (String fragment : dwucyfroweFragmenty) {

if (Integer.parseInt(fragment) > 90) {

licznik++;

}

System.out.println(licznik);

int[][] liczniki = new int[10][10]; // Inicjalizacja dwuwymiarowej tablicy liczników

// Obliczanie wystąpień każdego dwucyfrowego fragmentu

for (int i = 0; i < liczby.length - 1; i++) {

int x = dwucyfroweFragmenty[i].charAt(0) - '0'; // Pierwsza cyfra dwucyfrowego fragmentu

int y = dwucyfroweFragmenty[i].charAt(1) - '0'; // Druga cyfra dwucyfrowego fragmentu

liczniki[x][y]++; // Inkrementacja licznika dla odpowiedniego fragmentu

}

String minFragment = "00";

int minFragmentLiczba = liczniki[0][0];

String maksFragment = "00";

int maksFragmentLiczba = liczniki[0][0];

// Wyszukiwanie fragmentu o najmniejszej i największej liczbie wystąpień

for (int i = 0; i < 10; i++) {

for (int j = 0; j < 10; j++) {

if (liczniki[i][j] < minFragmentLiczba) {

minFragment = Integer.toString(i) + Integer.toString(j);

minFragmentLiczba = liczniki[i][j];

}

if (liczniki[i][j] > maksFragmentLiczba) {

maksFragment = Integer.toString(i) + Integer.toString(j);

maksFragmentLiczba = liczniki[i][j];

}

System.out.println(minFragment + " " + minFragmentLiczba);

System.out.println(maksFragment + " " + maksFragmentLiczba);

int indeks = 0;

licznik = 0;

// Sprawdzanie sekwencji rosnących i malejących liczb

while (indeks < liczby.length - 6) {

int[] lista = new int[6];

System.arraycopy(liczby, indeks, lista, 0, 6);

for (int j = 2; j < lista.length - 1; j++) {

if (czyRosnacy(lista, j) && czyMalejacy(lista, j)) {

licznik++;

break;

}

indeks++;

}

System.out.println(licznik);

int dlugosc = 6;

int maksIndeks = 0;

// Wyszukiwanie najdłuższej sekwencji rosnącej i malejącej

while (licznik > 0) {

indeks = 0;

licznik = 0;

while (indeks < liczby.length - dlugosc) {

int[] lista = new int[dlugosc];

System.arraycopy(liczby, indeks, lista, 0, dlugosc);

for (int j = 2; j < dlugosc - 1; j++) {

if (czyRosnacy(lista, j) && czyMalejacy(lista, j)) {

licznik++;

maksIndeks = indeks;

break;

}

indeks++;

}

dlugosc++;

}

System.out.println((maksIndeks + 1) + " ");

// Wyświetlanie najdłuższej sekwencji

for (int i = maksIndeks; i < maksIndeks + dlugosc - 2; i++) {

System.out.print(liczby[i]);

}

} catch (IOException e) {

e.printStackTrace(); // Wyświetlenie informacji o błędzie wejścia/wyjścia

}

// Sprawdzanie, czy ciąg liczb jest rosnący do określonego indeksu

static boolean czyRosnacy(int[] ciag, int koniec) {

for (int i = 1; i < koniec; i++) {

if (ciag[i - 1] >= ciag[i]) {

return false;

}

return true;

}

// Sprawdzanie, czy ciąg liczb jest malejący od określonego indeksu

static boolean czyMalejacy(int[] ciag, int start) {

for (int i = start + 1; i < ciag.length; i++) {

if (ciag[i - 1] <= ciag[i]) {

return false;

}

return true;

}

Zadanie 4 – Oceń prawdziwość podanych zdań

Matura z informatyki 2023 - zadanie 4 — Zadanie 4 – Oceń prawdziwość podanych zdań z arkusza maturalnego z informatyki maj 2023

Szyfrowanie asymetryczne polega na zastosowaniu 2 kluczy, czyli publicznego i prywatnego. Publiczny jak nazwa wskazuje jest ogólnodostępny i służy do szyfrowania wiadomości. Klucz prywatny jest dostępny tylko dla odbiorcy i służy do odszyfrowywania wiadomości.

Wiedząc to:

P – Wynika to wprost z definicji.
F – Zastanówmy się, jeśli klucz publiczny jest dostępny dla każdego, to nie mamy żadnej gwarancji, że osobą wysyłającą zaszyfrowaną wiadomość jest osoba B. Należy więc wybrać odpowiedź F.

Rozwiązanie:

Zadanie 5 – Systemy pozycyjne

Matura z informatyki 2023 - zadanie 5 — Zadanie 5 – Systemy pozycyjne z arkusza maturalnego z informatyki maj 2023

Przekonwertujmy wszystkie liczby na system dziesiętny, tak będzie najłatwiej je ze sobą porównać.

134₅ = 44₁₀,
134₆ = 58₁₀.

Jeśli nie chcemy tego robić manualnie, zawsze można to zrobić w pythonie np. print(int(“134”,5)), gdzie pierwszy argument to liczba a drugi to baza. Jak widać w pierwszym przykładzie należy wpisać znak “<”.

Drugi przykład rozwiązujemy analogicznie.

2222₃ = 80₁₀,
1111₆ = 259₁₀.

Więc tutaj również należy wstawić znak “<”.

Rozwiązanie:

(134)₅ < (134)₆

(2222)₃ < (1111)₆

Zadanie 6 – Konfitury owocowe

Matura z informatyki 2023 - zadanie 6 — Zadanie 6 – Konfitury owocowe z arkusza maturalnego z informatyki maj 2023

Zadanie konfitury sprawdza naszą wiedzę na temat arkuszy kalkulacyjnych. Najpierw działamy na pliku, a potem sami tworzymy symulację. Pierwsza część jest zazwyczaj prostsza i mniej czasochłonna, dlatego warto do niej podejść nawet, gdy średnio idą nam zadania oparte o Excela.

Na początek należy zaimportować dane. Najlepiej zaimportować dane do osobnego arkusza w którym nie będziemy nic zmieniać, dzięki temu mamy gwarancję, że nasze odpowiedzi nie będą złe z powodu przypadkowo zmodyfikowanych danych. Jeśli podpunkty nie są ze sobą powiązane, to je również warto dać do osobnych arkuszy do których wcześniej skopiowaliśmy dane.

Zadanie 6.1.

Należy zaznaczyć wszystkie dane, przejść do zakładki narzędzia główne i wybrać pole tabela przestawna. Lokalizacja w której umieścimy naszą tabelę jest dowolna, jednak najlepiej umieścić ją w tym samym arkuszu co dany podpunkt.

Rozwiązanie - matura z informatyki 2023 - zadanie 6.1 a — Tabela przestawna pozwoli na łatwe wykonanie zestawień.

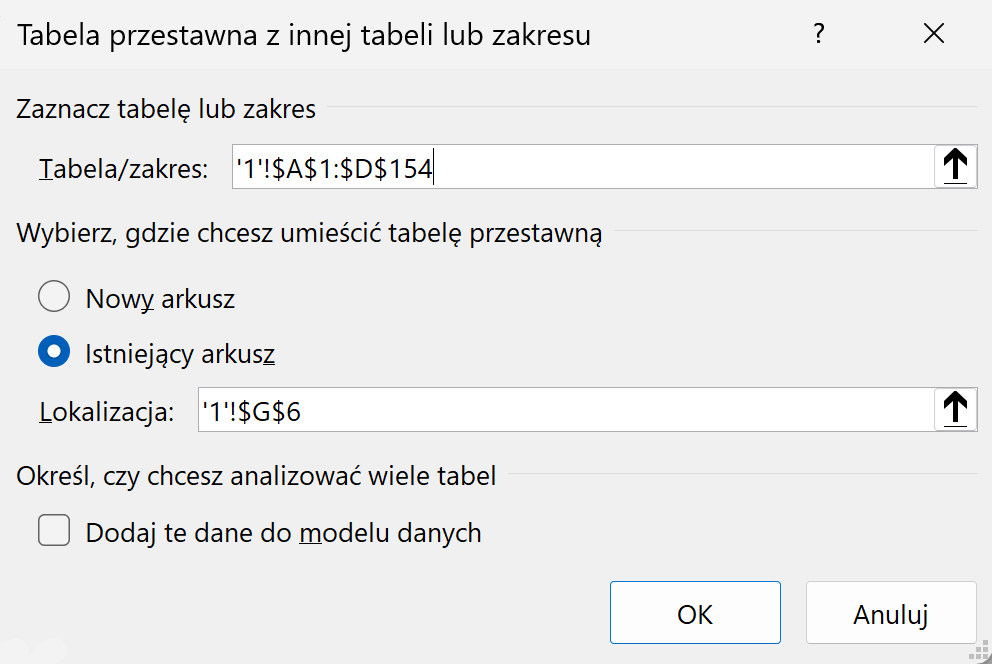
Rozwiązanie - Matura z informatyki 2023 - zadanie 6.1 b — Wybranie miejsca utworzenia tabeli przestawnej okazuje się łatwe do wykonania.

Następnie klikamy na nowo utworzoną tabelę i dodajemy do sekcji wiersze, kolumnę data. Doda to daty z dokładnością co do dnia. Należy usunąć wszystkie elementy oprócz miesiąca. Następnie do sekcji wartości dodajemy kolumny dostawa_porzeczek, dostawa_malin i dostawa_truskawek.

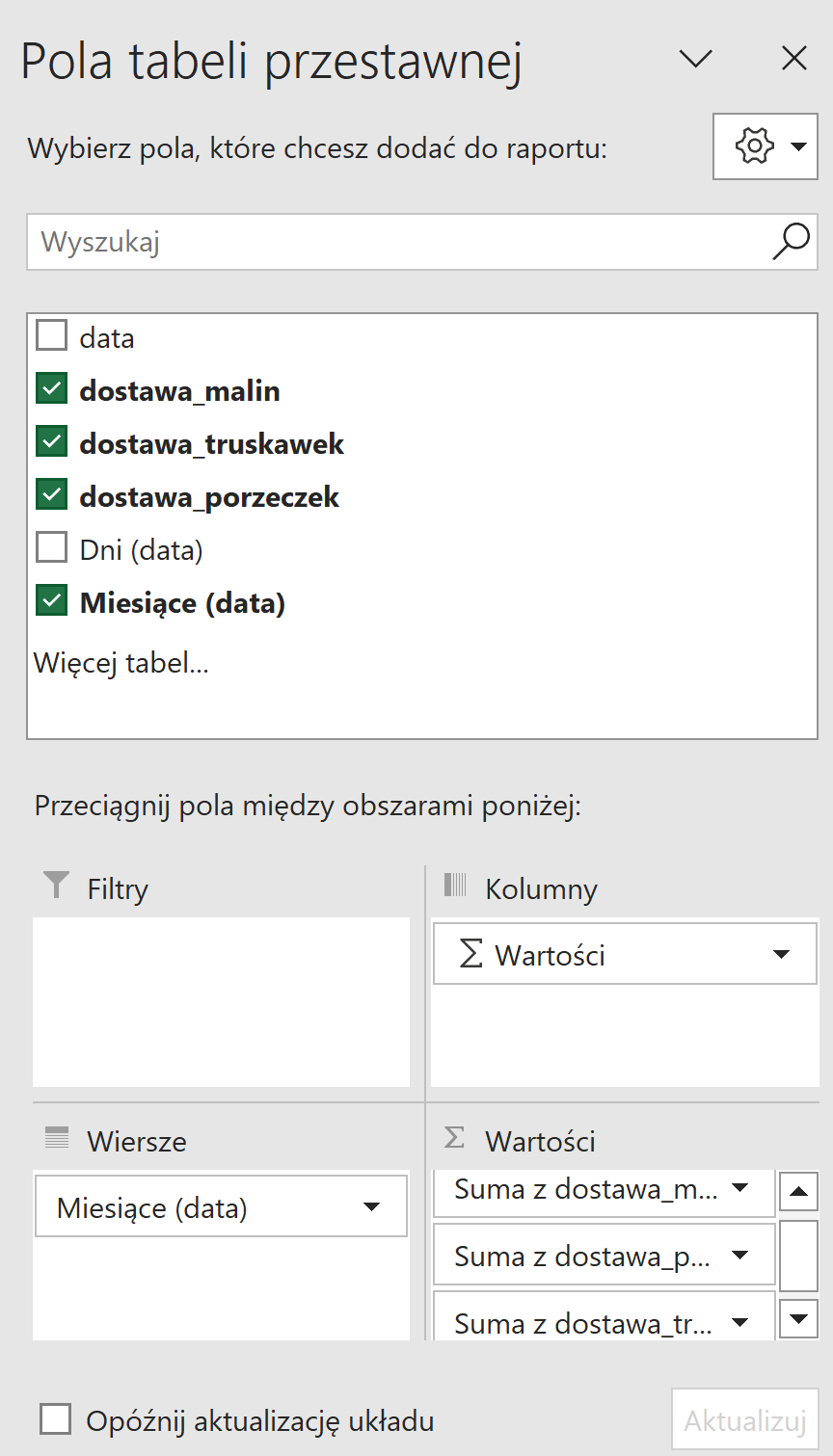
Rozwiązanie - Matura z informatyki 2023 - zadanie 6.1 c — Można dowolnie zmieniać pola wyświetlane w ramach raportu.

Zmieniamy też tytuły kolumn na takie, które pasują i usuwamy sumę końcową. Nasze zestawienie jest gotowe, teraz trzeba utworzyć wykres.

Rozwiązanie - Matura z informatyki 2023 - zadanie 6.1 d — Zmień tytuły kolumn na bardziej odpowiednie.

W tym celu zaznaczamy całą tabelę przestawną i w sekcji wstawianie klikamy przycisk polecane wykresy, a następnie wstawiamy wykres kolumnowy. Poprzez kliknięcie plusa, który pojawia się po wybraniu wykresu dodajemy elementy: tytuł wykresu, tytuły osi, legenda i ewentualnie etykiety danych (ta opcja czasem zasłania wykres). Teraz edytujemy nowo dodane elementy, żeby dobrze opisywały wartości.

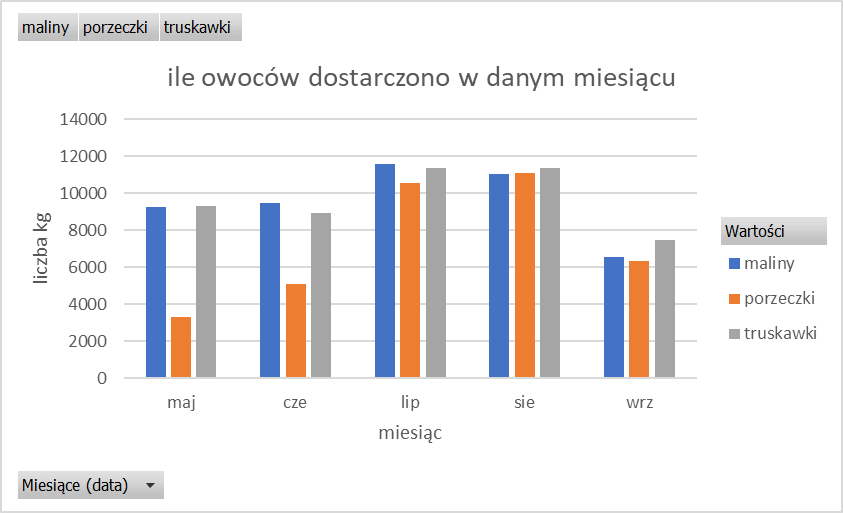
Podpunkt gotowy, teraz należy skopiować zestawienie do pliku z odpowiedzią i zapisać wykres w formacie obrazu.

Rozwiązanie:

miesiąc	dostawa_malin	dostawa_truskawek	dostawa_porzeczek
maj	9238	9287	3309
czerwiec	9485	8916	5081
lipiec	11592	11339	10567
sierpień	11045	11386	11386
wrzesień	6532	7476	6355

Zadanie 6.2.

Do naszych danych dodajemy nową kolumnę czyNajwiecejPorzeczek, w tej kolumnie używając funkcji JEŻELI oraz MAX sprawdzamy czy porzeczek w danym dniu było najwięcej. Porównujemy wartość maksymalną z wartością dostaw porzeczek, jeśli wartości są równe. To znaczy, że jeśli porzeczek było najwięcej, zwracamy do pola wartość 1,w przeciwnym razie wypisujemy wartość 0.

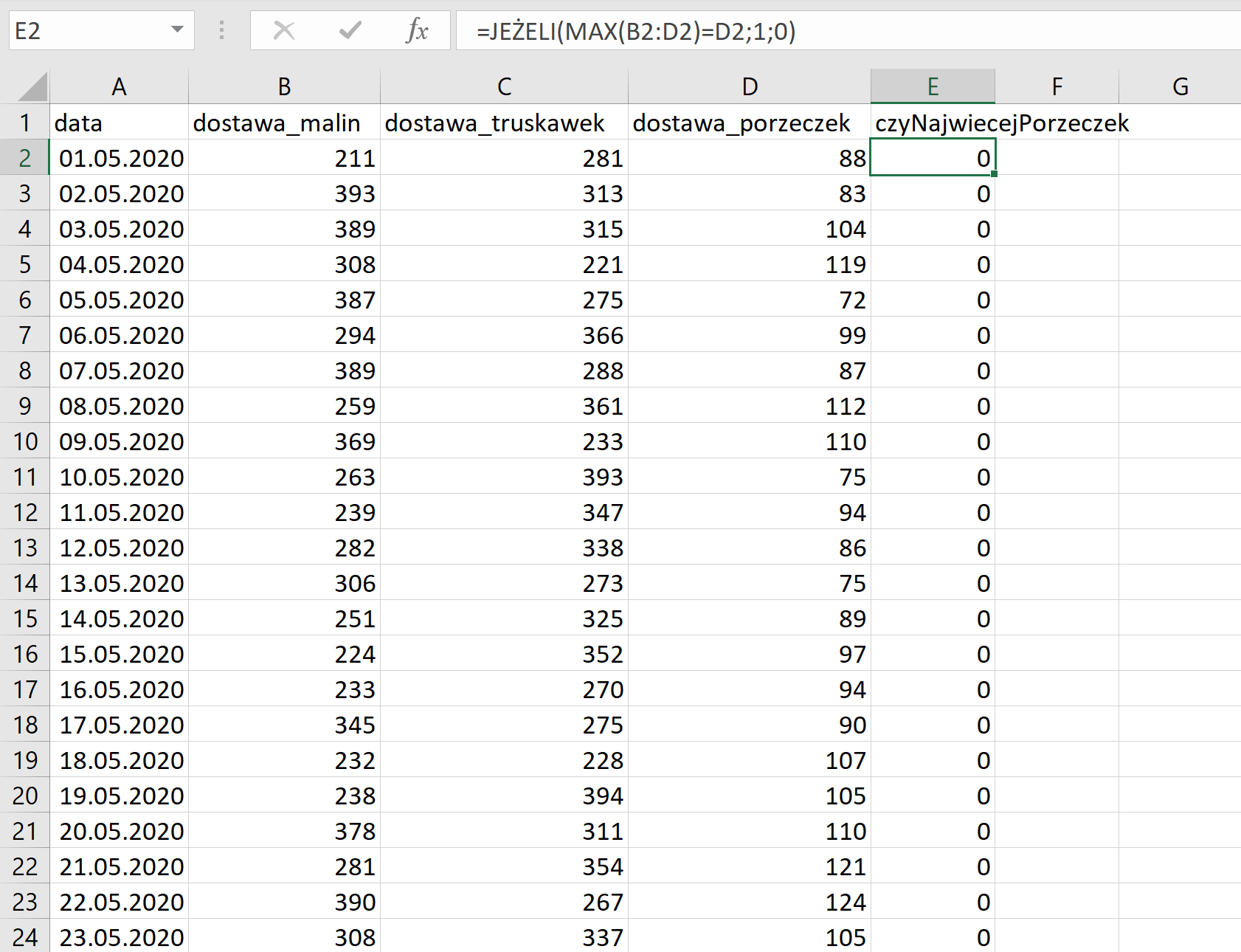
Rozwiązanie - Matura z informatyki 2023 - zadanie 6.2 a — W celu sprawdzenia dni z największą liczbą zebranych porzeczek należy skorzystać z polecenia JEŻELI(MAX(B2:D2)=D2;1;0).

Teraz używając funkcji SUMA lub LICZ.JEZELI zliczamy wystąpienia jedynek. Uzyskana liczba jedynek to nasza odpowiedź.

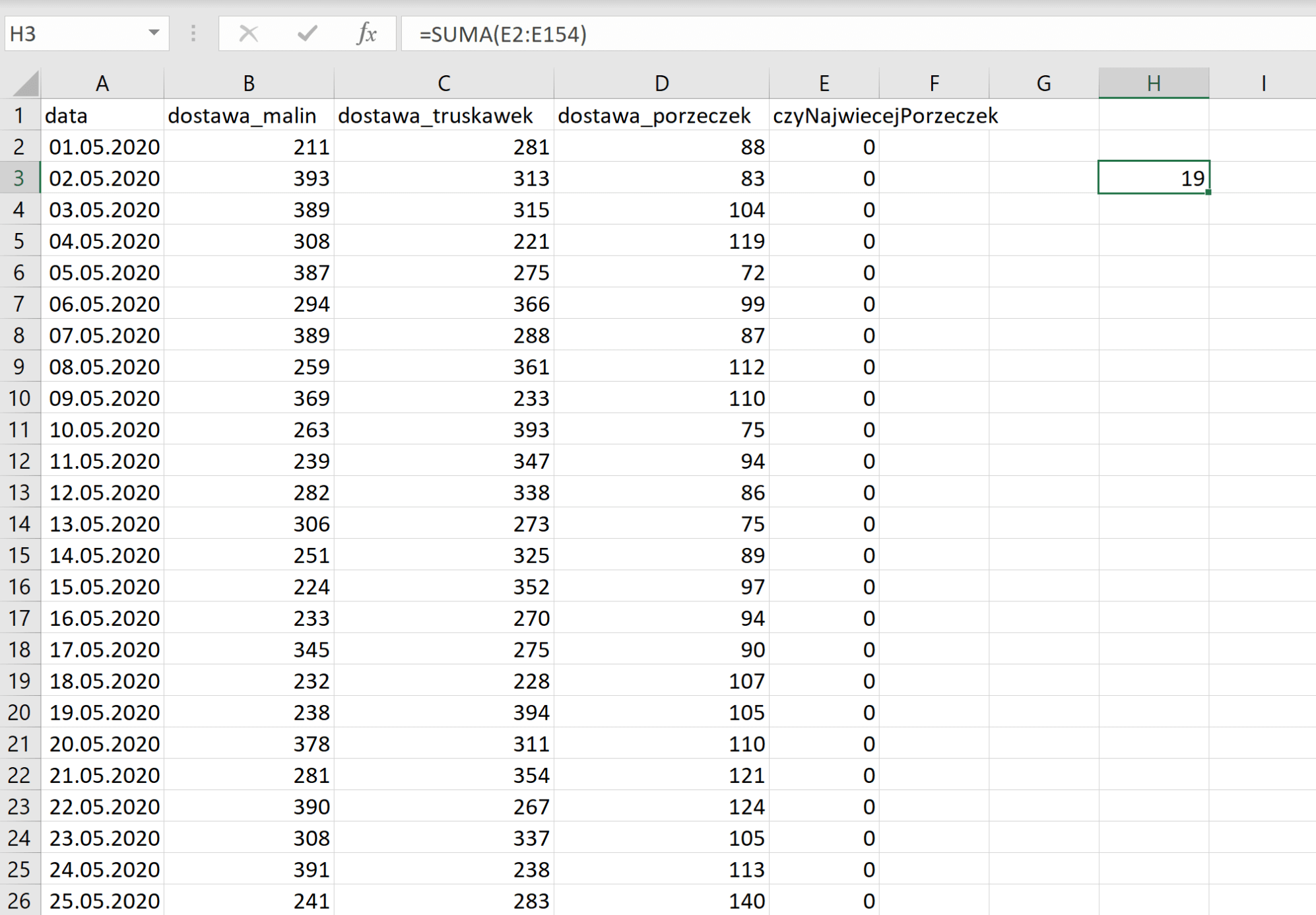
Rozwiązanie:

Zadanie 6.3.

Kolejne podpunkty opierają się na stworzonej przez nas symulacji. W nowym arkuszu do naszych danych dodajemy kolumny stan [owoc] rano dla każdego rodzaju owoców, kolumny ile [owoc] użyto oraz kolumny stan [owoc] po produkcji.

Pierwszy wiersz w kolumnach będzie trochę się różnił od pozostałych tak jak zazwyczaj w zadaniach tego typu. W kolumnach stan [owoc] rano, po prostu dajemy pole dostawy [owoc] tego dnia. W kolumnach ile [owoc] użyto, najpierw trzeba sprawdzić czy dany owoc w ogóle był używany, a jeśli tak to w jakiej ilości. Wiemy, że używane są owoce, których jest najwięcej oraz te drugie pod względem ilości. Zamiast dla każdego owocu sprawdzać czy jest go najwięcej lub prawie najwięcej, łatwiej sprawdzić czy danego owocu jest najmniej i dać do kolumny ile [owoc] użyto wartość zero. W przeciwnym razie wiemy, że danego owocu zużyto tyle samo co owocu, który jest drugi pod względem ilości.

Do znalezienia ile wynosi ta wartość, możemy użyć funkcji MAX.K, która znajduje którąś z kolei największą wartość (np. trzecią największą liczbę). Każda pole w kolumnie typu ile użyto powinna wyglądać mniej więcej tak: =JEŻELI(MIN($E3:$G3)=E3;0;MAX.K($E3:$G3;2)).

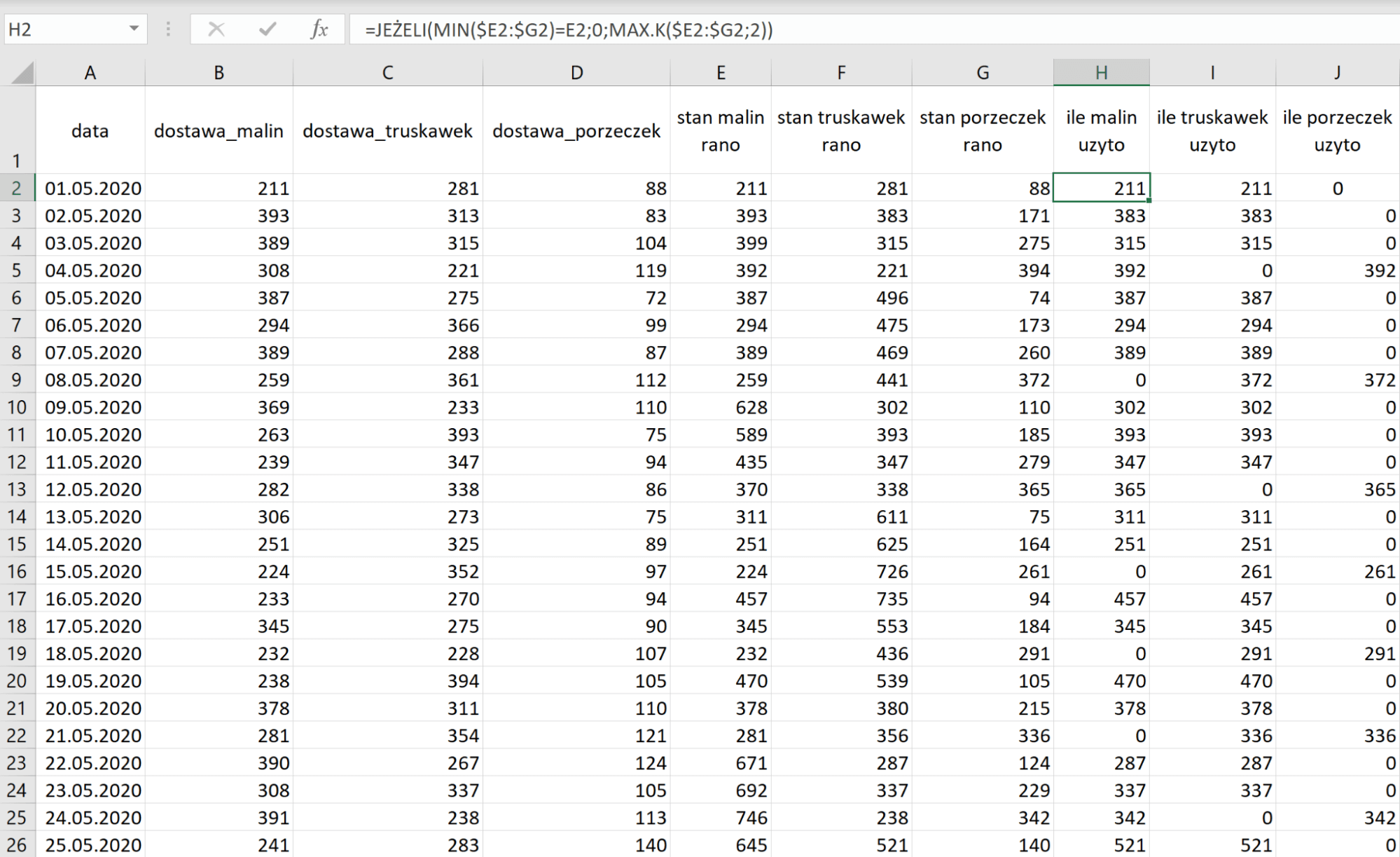
Rozwiązanie - Matura z informatyki 2023 - zadanie 6.3 a — Warunek =JEŻELI(MIN($E3:$G3)=E3;0;MAX.K($E3:$G3;2)) umożliwia sprawdzenie ile malin użyto.

Gdy wiemy ile użyto danego owocu danego dnia możemy do kolumn stan [owoc] po produkcji wstawiać różnicę stanu początkowego i wartości z kolumny ile [owoc] użyto.

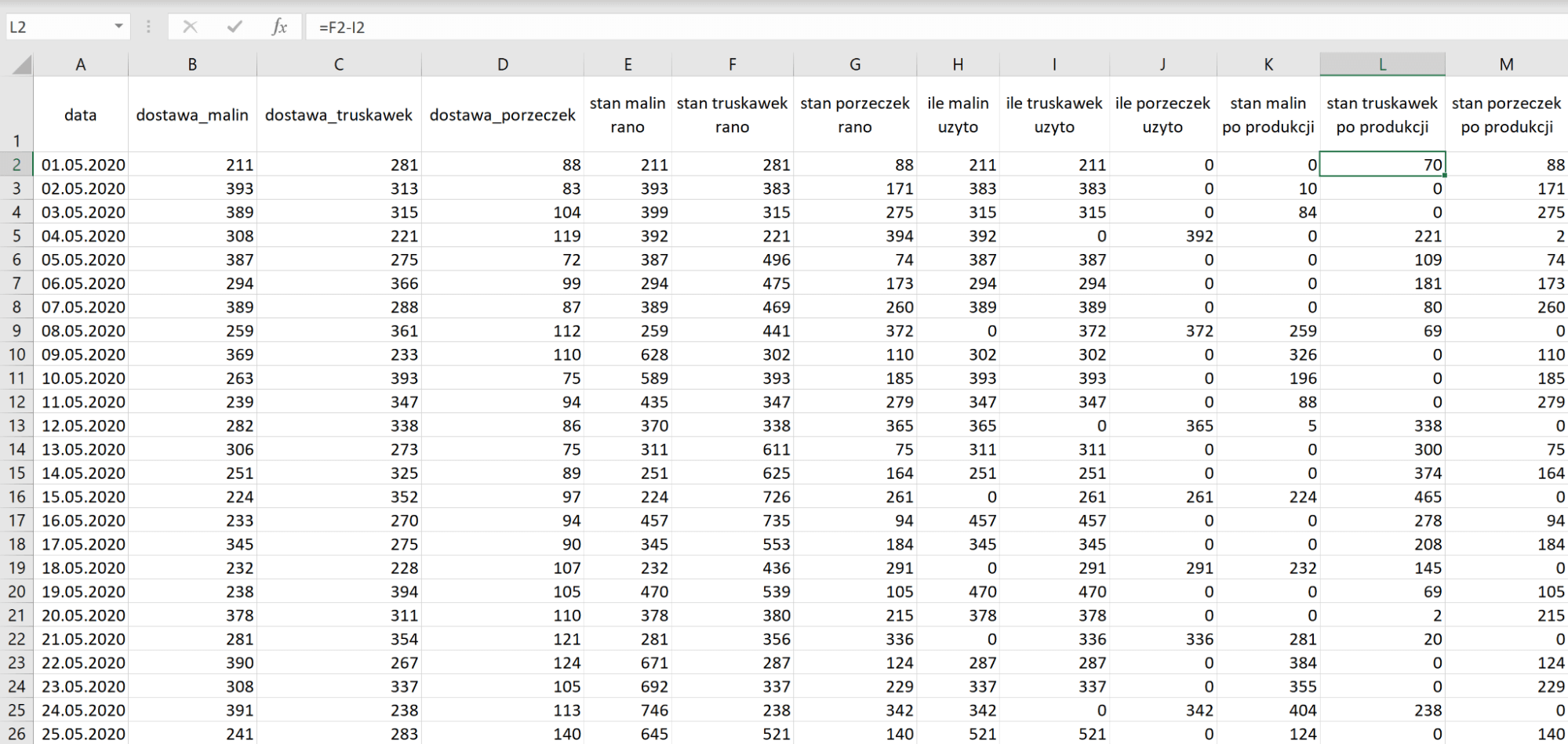
Rozwiązanie - Matura z informatyki 2023 - zadanie 6.3 b — Różnica między stanem początkowym, a ilością zużytą =F2-I2.

Kolejne wiersze naszej symulacji będą wyglądały dokładnie tak samo z drobną różnicą – zamiast ustawiać stan [owoc] rano na wartość dostawy ustawiamy ją na sumę dostawy i stanu po produkcji.

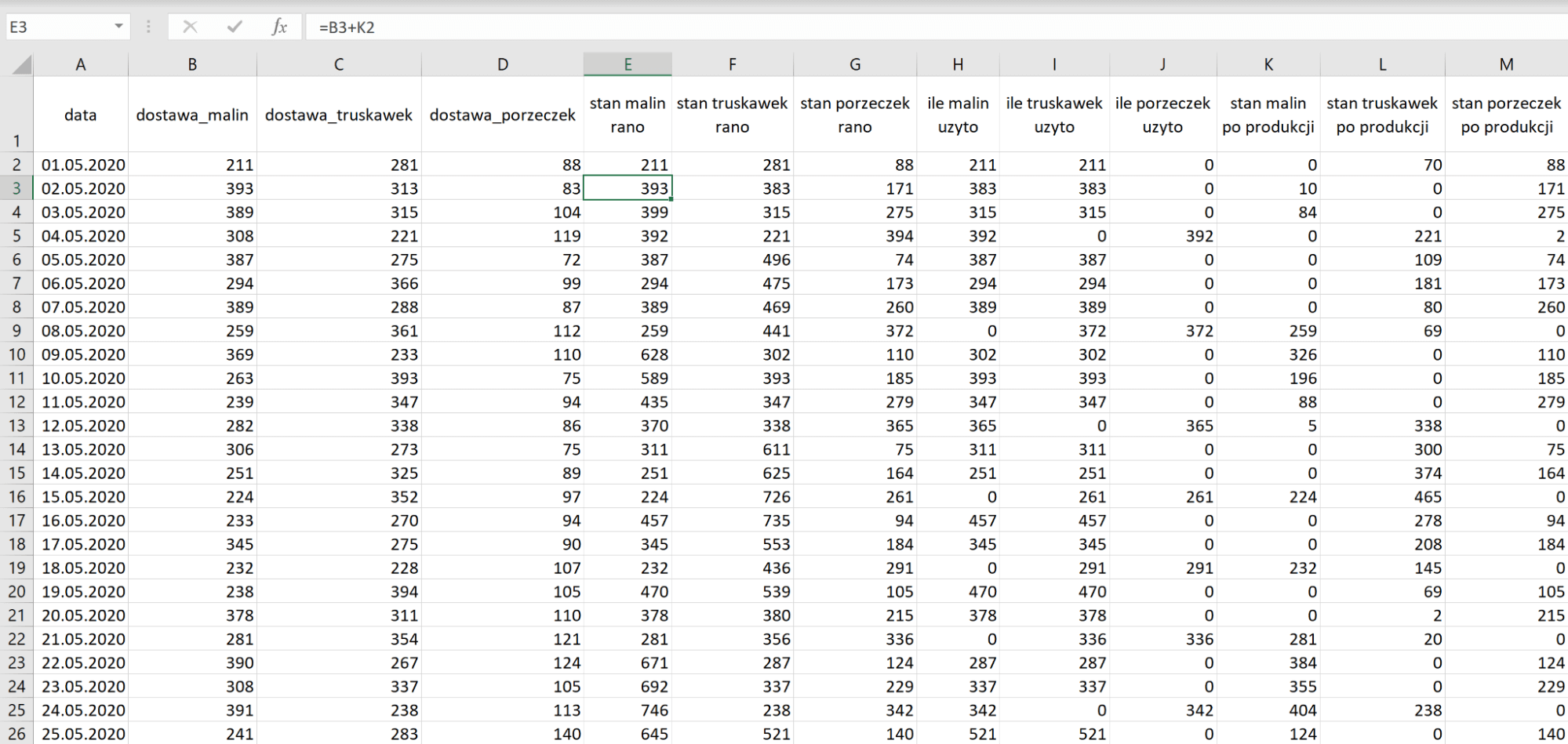
Rozwiązanie - Matura z informatyki 2023 - zadanie 6.3 c — Stan malin rano ustawia się na sumę dostawy malin i stanu malin po produkcji =B3+K2.

Teraz potrzebujemy określić rodzaj, dlatego wstawiamy nowy pusty pierwszy wiersz i nad porannym stanem każdego owocu wstawiamy jego pierwszą literę, czyli: m – maliny, t – truskawki i p – porzeczki. Następnie na końcu tabeli dodajemy nową kolumnę – rodzaj.

Ważne!
Funkcja X.WYSZUKAJ dostępna jest w Microsoft Excel od wersji 2021 oraz 365.

Do drugiego wiersza używając funkcji X.WYSZUKAJ (XLOOKUP) znajdujemy maksymalną wartość w kolumnach odpowiadających za poranny stan owoców i jako wynik zwracamy tabelę z pierwszego wiersza. Następnie kopiujemy funkcję i będąc cały czas w tej samej komórce, wstawiamy znak konkatenacji & (łączenia dwóch wyrażeń w jedno) i wklejamy funkcje, w tym zmieniamy MAX na MAX.K, gdzie k ustawiamy na 2. Komórka powinna zawierać teraz coś w tym stylu:

=X.WYSZUKAJ(MAX(E3:G3);E3:G3;$E$1:$G$1)&X.WYSZUKAJ(MAX.K(E3:G3;2);E3:G3;$E$1:$G$1).

To wyrażenie zwraca dwuliterowy skrót każdego rodzaju. Jest jednak pewien problem, zwraca ona 2 różne skróty dla każdego rodzaju np. mp i pm dla malinowo-porzeczkowego.

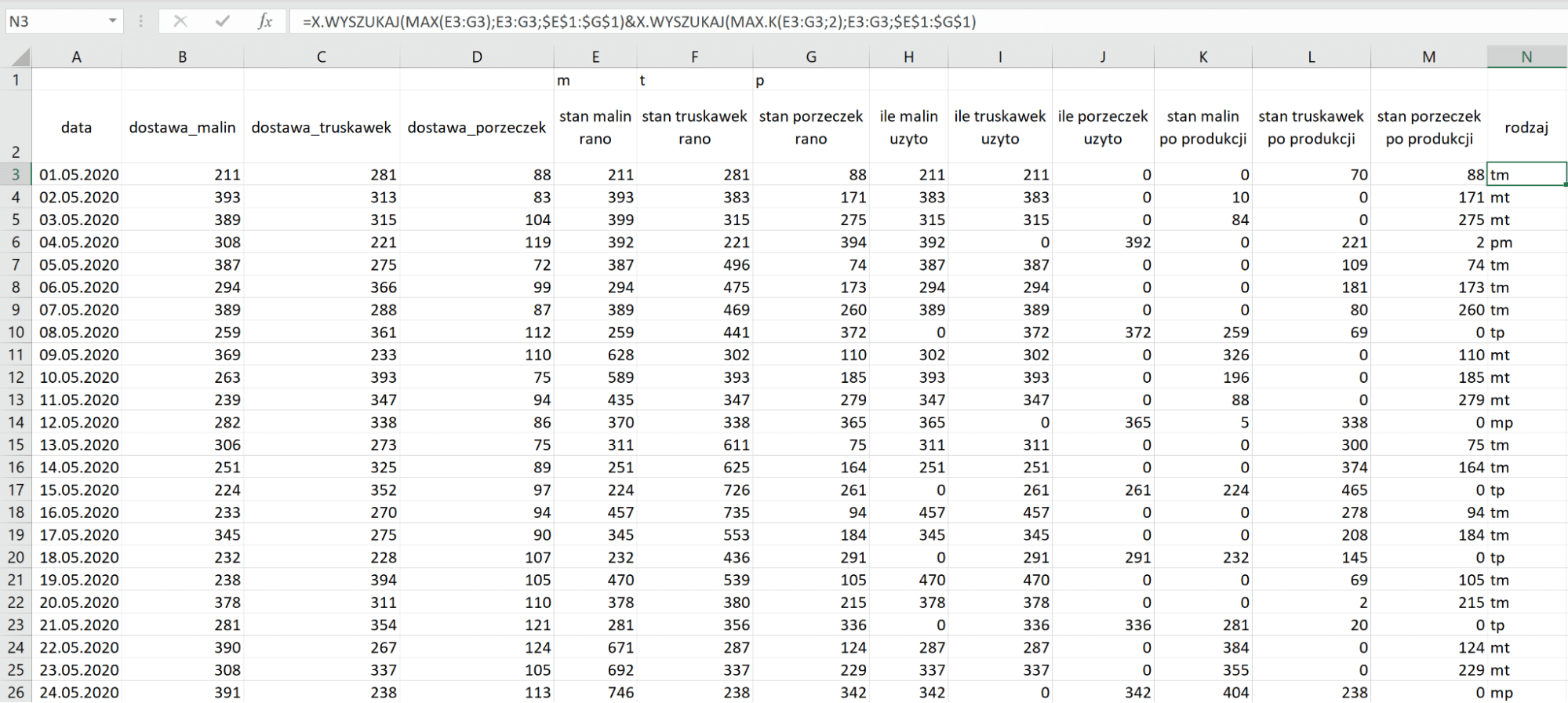
Rozwiązanie - Matura z informatyki 2023 - zadanie 6.3 d — Dwuliterowy skrót każdego rodzaju można zwrócić, dzięki użyciu funkcji =X.WYSZUKAJ(MAX(E3:G3);E3:G3;$E$1:$G$1)&X.WYSZUKAJ(MAX.K(E3:G3;2);E3:G3;$E$1:$G$1).

Na razie się tym nie przejmujemy i tworzymy tabelę przestawną z tylko jednej kolumny – tej zawierającej rodzaj (nie zaznaczaj pustych pól). Teraz dodajemy do części wiersz rodzaj, a także do kolumny wartości również rodzaj, teraz dla każdego dwuliterowego skrótu pojawi się liczba jego wystąpień.

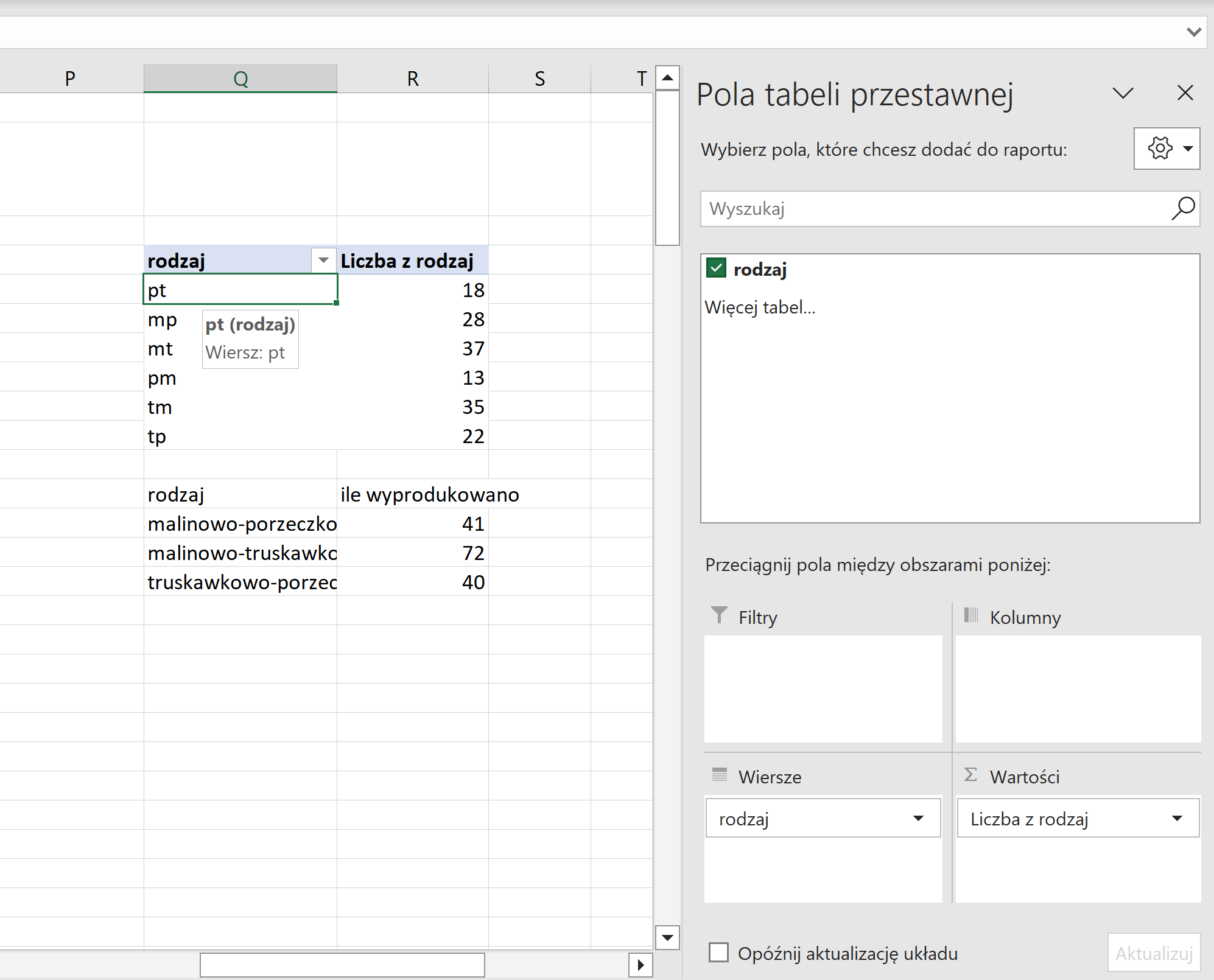
Niestety teraz musimy w trzech dowolnie wybranych wierszach manualnie wpisać nazwy rodzajów i obok każdej z nich wstawić sumę dwóch pól z tabeli przestawnej odpowiadających danemu dżemowi. Podpunkt jest już gotowy.

Rozwiązanie:

malinowo-porzeczkowe 41
malinowo-truskawkowe 72
truskawkowo-porzeczkowe 40

Zadanie 6.4.

Ostatni podpunkt opiera się na naszych obliczeniach z podpunktu 3, więc też jest już prawie gotowy. Dodajemy do naszej tabeli nową kolumnę – ile kg konfitury wyprodukowano. Żeby to sprawdzić wystarczy użyć funkcji MAX na kolumnach typu ile użyto. NIe trzeba jej mnożyć lub dzielić, czy czegoś dodawać. Wiemy przecież, że w przypadku każdego owocu, którego używano, wykorzystano dokładnie tyle samo kilogramów, a że i tak musimy podzielić wartość na 2, żeby uzyskać wynik, można te działania po prostu ominąć.

Wszystko jest już gotowe do tworzenia zestawienia. Tworzymy tabelę przestawną z kolumnami rodzaj oraz nowo dodaną kolumną. Do sekcji wiersze dodajemy rodzaj, a drugą kolumnę dodajemy do sekcji wartości. Na koniec należy zrobić prawie to samo co w poprzednim podpunkcie, czyli wpisać nazwy dżemów i zsumować odpowiadające im wartości.

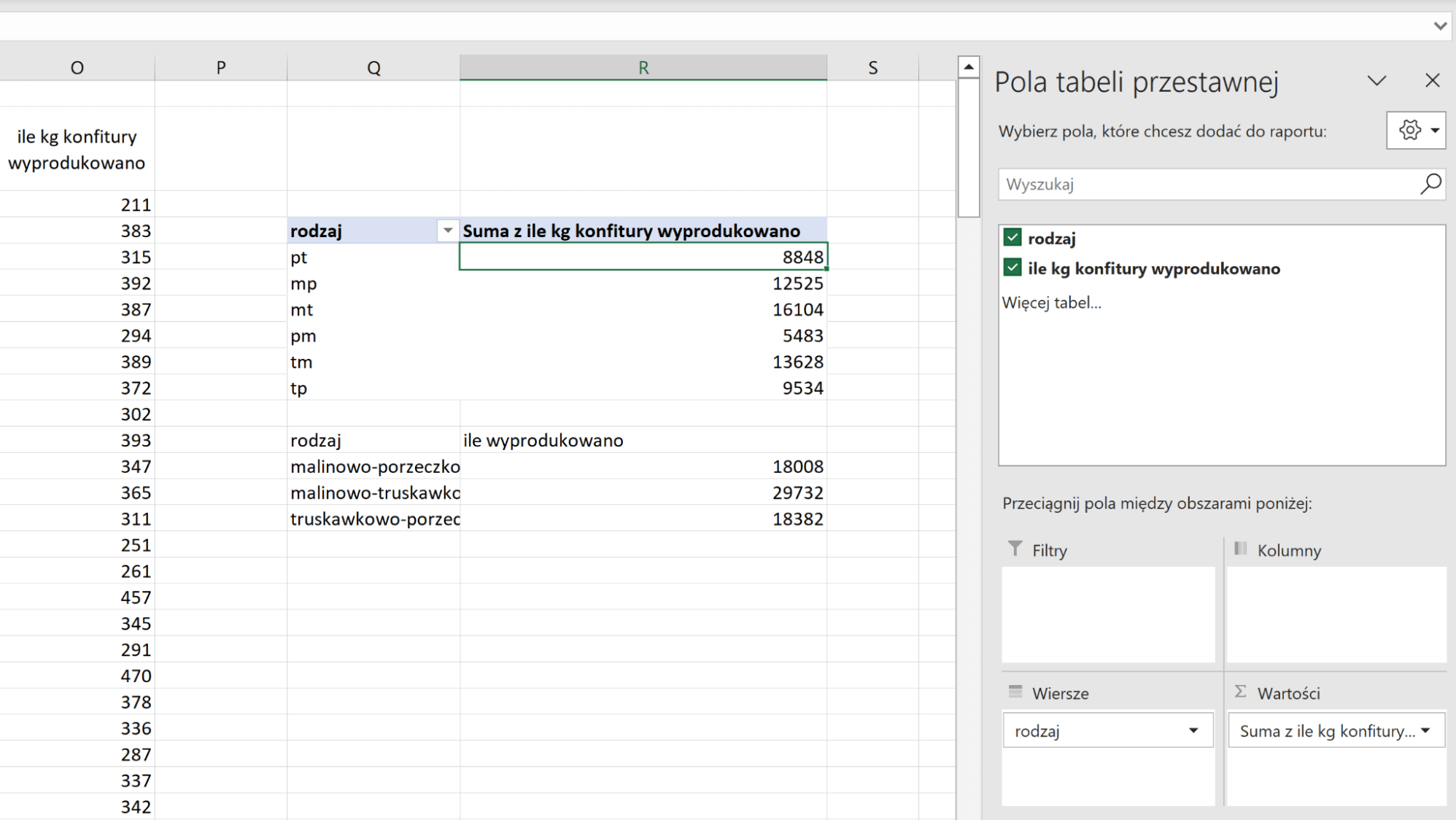
Rozwiązanie:

malinowo-porzeczkowe 18008
malinowo-truskawkowe 29732
truskawkowo-porzeczkowe 18382

Zadanie 7 – Gry planszowe

Matura z informatyki 2023 - zadanie 7 — Zadanie 7 – Gry planszowe z arkusza maturalnego z informatyki maj 2023

Na koniec typowe polecenie dotyczące baz danych. W tego typu zadaniach musimy na samym początku poprawnie zaimportować dane z plików do accessa. Jeśli coś źle zaimportujemy możliwe, że całe zadanie będzie złe, dlatego trzeba wszystko dokładnie sprawdzić.

Wyjątkiem jest tutaj plik oceny.txt ponieważ nie zawiera on pola, które mogłoby być kluczem podstawowym, dlatego należy wybrać opcję Pozwalaj programowi Access dodać klucz podstawowy. Teoretycznie można utworzyć tabelę bez id dla każdego elementu, ale jest to zły pomysł.

Zadanie 7.1.

Do pierwszego podpunktu należy utworzyć kwerendę, wystarczy kliknąć Projekt kwerendy w zakładce Tworzenie.

Rozwiązanie - Matura z informatyki 2023 - zadanie 7.1 a — W celu utworzenia kwerendy należy kliknąć Tworzenie/Projekt kwerendy.

Żeby dodać do kwerendy tabele z których chcemy wybierać dane, musisz posłużyć się znanym Ci już panelem bocznym.

W podpunkcie mamy podać tytuł gry, który znajduje się w tabeli Gry i liczbę ocen wystawionych tej grze, z kolei tą informację można uzyskać z tabeli Oceny. Trzeba więc dodać te tabele i wybrać z nich kolumny Gry.id_gry, Gry.nazwa oraz dowolną kolumnę z tabeli Oceny. Jednak żeby zamiast informacji zawartych w tej kolumnie uzyskać liczbę wierszy, w których dane id_gry występują należy użyć sum, a konkretnie funkcji Policz. Włączenie sum jest dość proste, wystarczy kliknąć przycisk Sumy w zakładce Projekt kwerendy.

Rozwiązanie - Matura z informatyki 2023 - zadanie 7.1 b — W celu użyciu sum (funkcji policz), należy kliknąć Projekt kwerendy/Sumy.

Następnie zmienimy suma z Grupuj według na policz w kolumnie kwerendy, która bierze dane z tabeli Oceny, a w pozostałych pozostawiamy Grupuj według. Taka konfiguracja sprawia, że wiersze w których są te same dane, łączą się ze sobą (dzięki Grupuj według), liczba tych wierszy jest zliczana funkcją policz. Na koniec wystarczy posortować malejąco według kolumny, która zlicza wystąpienia.

To sprawi, że gra o największej liczbie wystąpień, pojawi się na samej górze i będzie ją można łatwo odnaleźć. Teraz odpowiedź jest oczywista, wystarczy skopiować ją do pliku txt podanego w poleceniu (oczywiście tylko i wyłącznie wskazane kolumny). Teraz pewnie zastanawiasz się po co w ogóle było to pole id_gry? A no po to, że dwie różne gry mogły mieć ten sam tytuł, a bez brania pod uwagę id zostałyby one połączone w jedną, przez co ich liczba wystąpień byłaby zsumowana, więc skutkowałaby niepoprawną odpowiedzią. Pamiętaj, aby zawsze tak robić w zadaniach, gdy trzeba policzyć ilość pól, ten trik jest bardzo często stosowany przez CKE. Po rozwiązaniu podpunktu, zawsze zapisuj kwerendy, które były wykorzystane do jego rozwiązania, bo na maturze musisz mieć dowód na utworzenie odpowiedzi.

Implementacja – SQL

SELECT Gry.id_gry, Gry.nazwa, Count(Oceny.Identyfikator) AS PoliczOfIdentyfikator
FROM Gry INNER JOIN Oceny ON Gry.id_gry = Oceny.id_gry
GROUP BY Gry.id_gry, Gry.nazwa
ORDER BY Count(Oceny.Identyfikator) DESC;

SELECT Gry.id_gry, Gry.nazwa, Count(Oceny.Identyfikator) AS PoliczOfIdentyfikator

FROM Gry INNER JOIN Oceny ON Gry.id_gry = Oceny.id_gry

GROUP BY Gry.id_gry, Gry.nazwa

ORDER BY Count(Oceny.Identyfikator) DESC;

Rozwiązanie:

Zadanie 7.2.

W następnym podpunkcie znowu korzystamy tylko z tabel Gry i oceny. Potrzebujemy id_gry, nazwa oraz kategoria i pola ocena z tabeli Oceny. Tak samo jak w pierwszym podpunkcie włączamy sumy, lecz tym razem zamiast policz dajemy średnią. Teraz pewnie wiesz, dlaczego w pierwszym podpunkcie pole może być dowolne – nie ma znaczenia co liczymy, jednak przy średniej ma to ogromne znaczenie. Nasze zadanie jest prawie gotowe, musimy dać jeszcze kryterium na kolumnę kategoria, dajemy więc “imprezowa” (razem z cudzysłowem!) do pola kryterium. Cudzysłowy są potrzebne, inaczej Access potraktowałby to co wpisaliśmy jako zmienną.

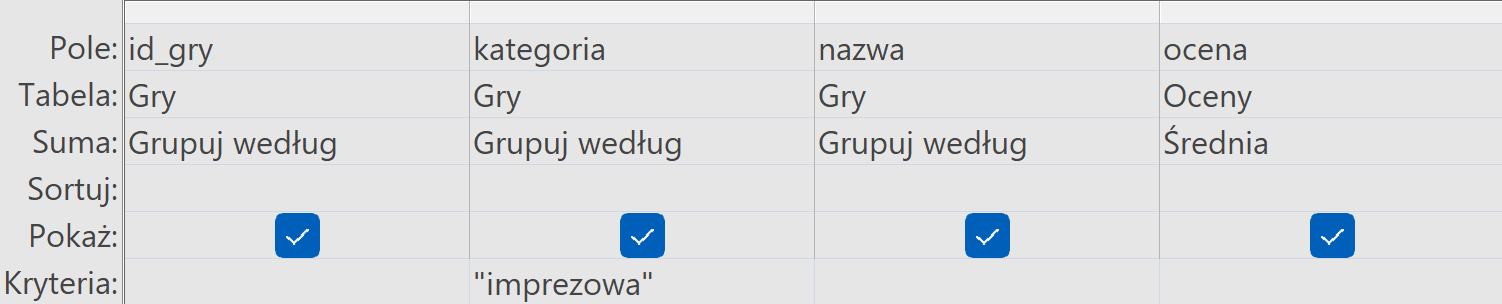
Rozwiązanie - Matura z informatyki 2023 - zadanie 7.2 a — Po uruchomieniu sum, należy skorzystać z funkcji średnia. Dodatkowo na kolumnę kategoria dodaje się “imprezowa” (razem z cudzysłowem) do pola kryterium.

Ostatnią rzeczą, o którą jesteśmy proszeni w zadaniu jest ustawienie dokładności średniej na 2 miejsca po przecinku. Należy kliknąć prawym przyciskiem myszy na jedno z pól edycji kolumny, które liczy średnią i wybrać właściwości.

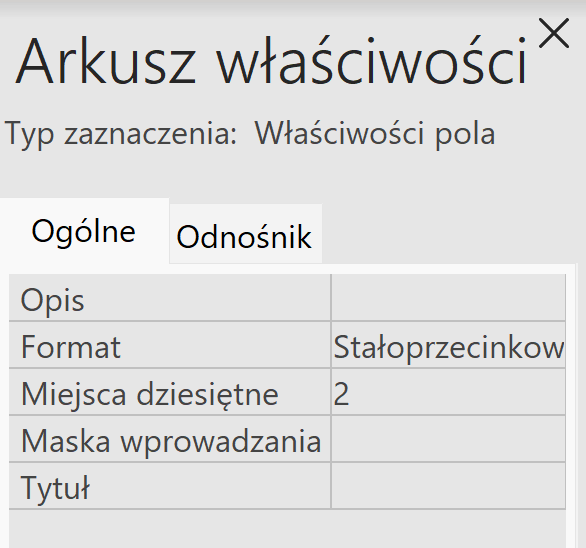
Rozwiązanie - Matura z informatyki 2023 - zadanie 7.2 b — Na jednym z pól edycji kolumny liczących średnią kliknij PPM/Właściwości i zmodyfikuj powyższe pola.

Otworzy się wtedy panel boczny w którym format ustawiamy na stałoprzecinkowy, a miejsca dziesiętne na 2. Voilá, podpunkt gotowy.

Implementacja – SQL

SELECT Gry.id_gry, Gry.kategoria, Gry.nazwa, Avg(Oceny.ocena) AS ŚredniaOfocena
FROM Gry INNER JOIN Oceny ON Gry.id_gry = Oceny.id_gry
GROUP BY Gry.id_gry, Gry.kategoria, Gry.nazwa
HAVING (((Gry.kategoria)="imprezowa"));

SELECT Gry.id_gry, Gry.kategoria, Gry.nazwa, Avg(Oceny.ocena) AS ŚredniaOfocena

FROM Gry INNER JOIN Oceny ON Gry.id_gry = Oceny.id_gry

GROUP BY Gry.id_gry, Gry.kategoria, Gry.nazwa

HAVING (((Gry.kategoria)="imprezowa"));

Rozwiązanie:

nazwa Średnia ocena

5 sekund 8,16

Avalone 8,25

Colt Express 7,54

Jenga 8,16

Koncept 8,37

Mamy szpiega 8,22

Przebiegle wielblady 7,73

Sushi Go 8,07

Swiatowy Konflikt 7,80

Szeryf z Nottingham 7,88

Zadanie 7.3.

Trzeci podpunkt jest trochę bardziej skomplikowany. Na początek znajdźmy graczy, którzy wystawili jakąś ocenę, w tym celu wystarczy stworzyć kwerendę w której użyjemy tabeli gracze oraz Oceny. Wystarczy pobrać teraz pole id_gracza z dowolnej tabeli, włączyć sumy, żeby nie było duplikatów i zapisać. To będzie nasza kwerenda pomocnicza.

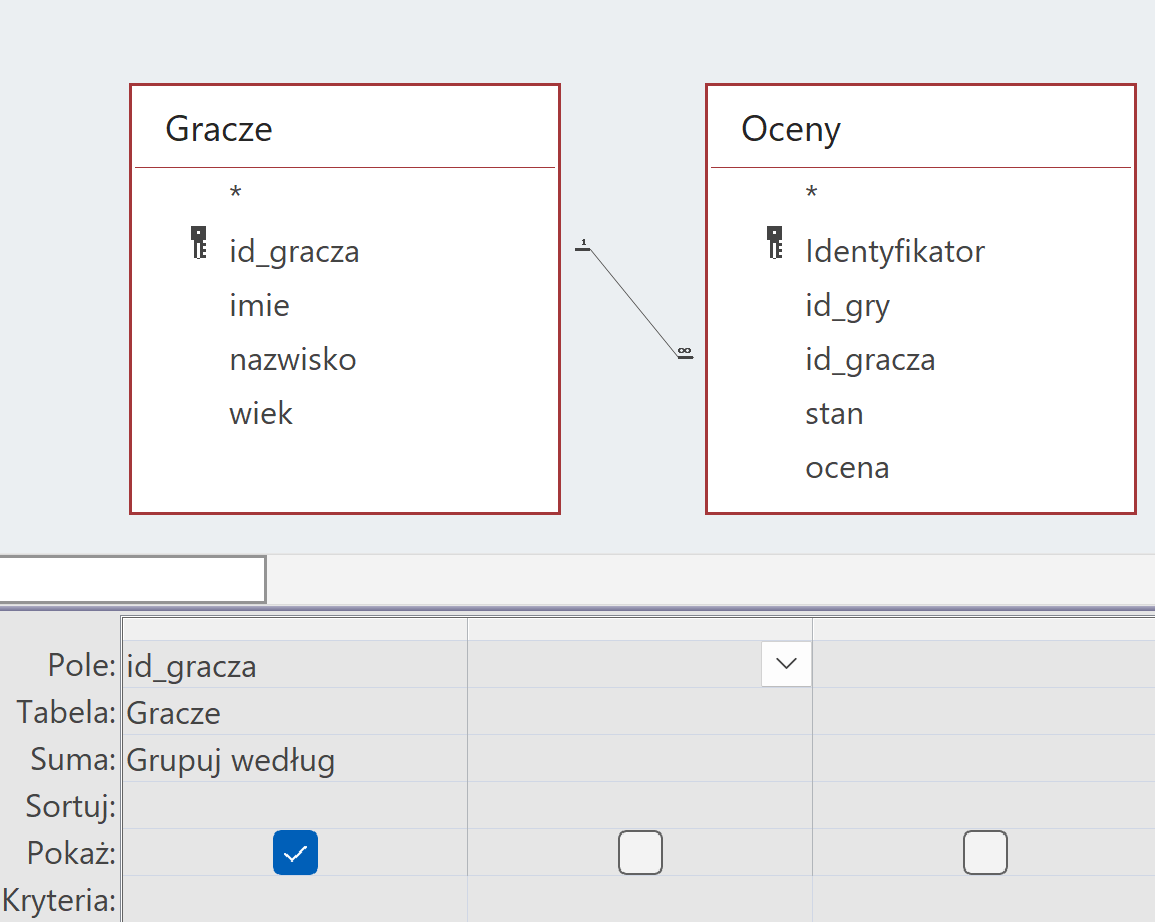
Rozwiązanie - Matura z informatyki 2023 - zadanie 7.3 a — Utworzenie kwerendy pomocniczej.

Implementacja – SQL

SELECT Gracze.id_gracza
FROM Gracze INNER JOIN Oceny ON Gracze.id_gracza = Oceny.id_gracza
GROUP BY Gracze.id_gracza;

SELECT Gracze.id_gracza

FROM Gracze INNER JOIN Oceny ON Gracze.id_gracza = Oceny.id_gracza

GROUP BY Gracze.id_gracza;

Następnie tworzymy kwerendę w której liczymy jak wiele ocen dany gracz wystawił grom, które posiada. Używamy do tego tabeli gracze i oceny. Potrzebujemy do tego id_gracza z wierszem suma o wartości grupuj według dowolnego pola z tabeli Oceny z funkcją policz oraz kolumny Oceny.stan z wierszem suma o wartości gdzie oraz kryterium “posiada”. Wiersz suma z wartością gdzie, to wcale nie jest suma, tylko po prostu kryterium WHERE znane ze SQL, jednak tak jest to zaimplementowane w accessie. Teraz mając te dwie kwerendy patrzymy na liczbę wierszy w każdej z nich, można to sprawdzić w lewym dolnym rogu w trybie wyświetlania kwerendy. Wystarczy odjąć od liczby graczy wystawiających ocenę – liczbę graczy z drugiej kwerendy pomocniczej.

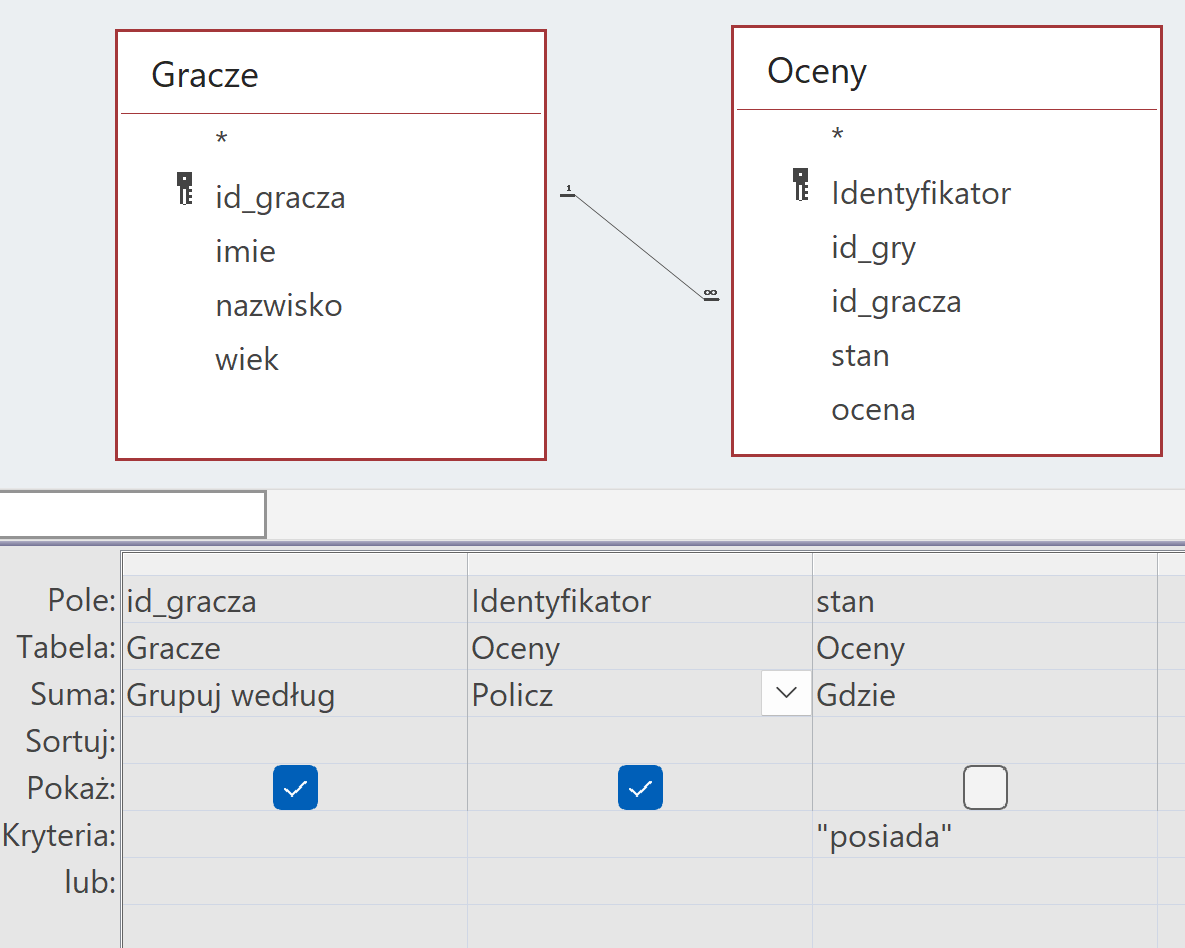
Rozwiązanie - Matura z informatyki 2023 - zadanie 7.3 b — Posiadając dwie kwerendy można wykonać odpowiednie obliczenia.

Implementacja: do kwerendy – SQL

SELECT Gracze.id_gracza, Count(Oceny.Identyfikator) AS PoliczOfIdentyfikator
FROM Gracze INNER JOIN Oceny ON Gracze.id_gracza = Oceny.id_gracza
WHERE (((Oceny.stan)="posiada"))
GROUP BY Gracze.id_gracza;

SELECT Gracze.id_gracza, Count(Oceny.Identyfikator) AS PoliczOfIdentyfikator

FROM Gracze INNER JOIN Oceny ON Gracze.id_gracza = Oceny.id_gracza

WHERE (((Oceny.stan)="posiada"))

GROUP BY Gracze.id_gracza;

Rozwiązanie:

334

Zadanie 7.4.

Na początek stwórzmy tabelę, która każdemu id gracza przyporządkowuje jego kategorię wiekową. Tworzymy więc kwerendę, dodajemy do niej id_gracza z tabeli Gracze oraz tworzymy wyrażenie klikając prawym przyciskiem myszy w puste pole obok, w wierszu Pole: i wybierając opcję konstruuj. Wpisujemy tam takie wyrażenie IIf([Gracze].[wiek]<20;”junior”;IIf([Gracze]![wiek]<50;”senior”;”weteran”)) i klikamy OK.

Używamy tutaj funkcji iif i to 2 razy, działa ona tak – pierwszy argument to warunek, a dwa pozostale to sytuacje kiedy warunek jest spełniony lub nie. Najpierw patrzymy czy wiek gracza jest mniejszy od 20, jeśli nie to znowu używamy funkcji iif i sprawdzamy czy nasz gracz nie jest czasem w przedziale wiekowym seniora, jeśli nie to zostaje nam tylko jedna opcja – weteran.

Implementacja: do kwerendy – SQL

SELECT Gracze.id_gracza, IIf([Gracze].[wiek]<20,"junior",IIf([Gracze]![wiek]<50,"senior","weteran")) AS Wyr1
FROM Gracze;

1 2	SELECT Gracze.id_gracza, IIf([Gracze].[wiek]<20,"junior",IIf([Gracze]![wiek]<50,"senior","weteran")) AS Wyr1 FROM Gracze;

Następnie tworzymy kwerendę, dodajemy do niej tabele Oceny oraz Gry i kwerendę, którą przed chwilą stworzyliśmy. Gdy dodajemy kwerendę trzeba utworzyć relacje po prostu przeciągając pole Oceny.id_gracza do odpowiadającego mu pola z kwerendy pomocniczej. Wybieramy kolumny: nasze wyrazenie z grupuj wedlug, id_gry z grupuj wedlug, nazwa gry z grupuj według oraz dowolne pole z ocen o posiadające policz. Warto też dać sortowanie malejące na kolumnę z policz. Teraz już wszystko jest gotowe, wystarczy znaleźć dla każdej kategorii wiekowej jej pierwsze wystąpienie, sprawdzić czy nie ma kilku o tej samej liczbie wystąpień i już. Dla ułatwienia można za każdym razem zmieniać kryterium kategorii.

Implementacja: do kwerendy – SQL

SELECT Gracze.id_gracza, IIf([Gracze].[wiek]<20,"junior",IIf([Gracze]![wiek]<50,"senior","weteran")) AS Wyr1
FROM Gracze;

1 2	SELECT Gracze.id_gracza, IIf([Gracze].[wiek]<20,"junior",IIf([Gracze]![wiek]<50,"senior","weteran")) AS Wyr1 FROM Gracze;

Rozwiązanie:

Kategoria Tytuł gry Liczba ocen

juniorzy Terraformacja Marsa 6

juniorzy K2 6

seniorzy K2 24

weterani Robinson Crusoe 28

Zadanie 7.5.

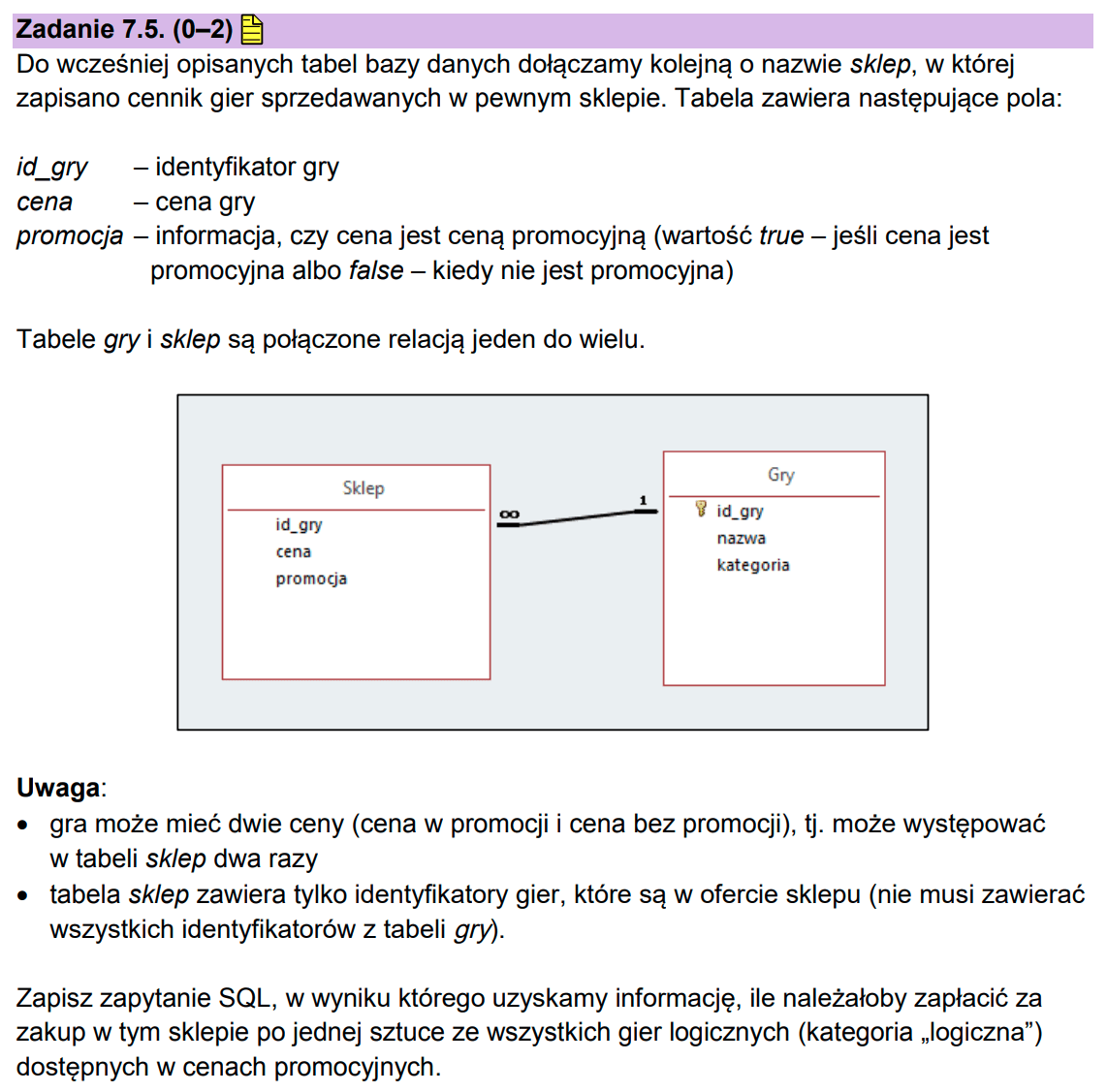
Kolejne zadanie jest stworzone do rozwiązywania na kartce, ale to nie znaczy że komputer nie będzie już przydatny. Znając różnice między standardowym SQL-em, a SQL-em w Accessie (JET SQL) bardzo łatwo można przepisać prawie gotową odpowiedź z Accessa.

Tworzymy nową tabelę o nazwie Sklep (zakładka tworzenie/tabela, bardzo podobnie do kwerendy). Wchodzimy w tryb edycji usuwamy istniejące pola i dodajemy nowe pola tak jak w poleceniu, czyli id_gry – liczba, cena gry – liczba i ostatnie pole ma typ boolean, tego typu nie ma w Accessie, ale tym się nie przejmujemy i dajemy typ krótki tekst. Możemy dodać też parę rekordów, żeby widzieć, czy nasze kwerendy będą działać.

Rozwiązanie - Matura z informatyki 2023 - zadanie 7.5 a — Skorzystanie z pomocy Accessa ułatwia rozwiązanie zadania, mimo że jest ono przeznaczone do opisania na kartce.

Teraz tworzymy naszą kwerendę, dodajemy tabelę Gry oraz nowo utworzoną tabelę Sklep. Tworzymy między nimi relację z pomocą id_gry. Dodajemy pole cena z sumą Suma, pole kategoria z sumą gdzie i kryterium “logiczna” oraz pole promocja z sumą Gdzie i kryterium “true”. Teraz przechodzimy do widoku SQL. Najlepiej teraz skopiować wszystko do notatnika i tam dokonać edycji. JET SQL różni się głównie tym, że są w nim bardzo duże ilości niepotrzebnych nawiasów. Po prostu usuwamy wszystkie nawiasy poza tymi dotyczącymi funkcji. Musimy też usunąć cudzysłów znajdujący się nad true, bo w SQL to jest boolean, a nie string. Warto też usunąć nazwę kolumny kwerendy, bo o ile w Accesie jest ona wymagana to w standardowym już nie, a autorzy zadanie nic o tym nie wspominają.
Implementacja – SQL

Czyli z tego:

SELECT Sum(Sklep.cena) AS SumaOfcena
FROM Sklep INNER JOIN Gry ON Sklep.id_gry = Gry.id_gry
WHERE (((Gry.kategoria)="logiczna") AND ((Sklep.promocja)="true"));

SELECT Sum(Sklep.cena) AS SumaOfcena

FROM Sklep INNER JOIN Gry ON Sklep.id_gry = Gry.id_gry

WHERE (((Gry.kategoria)="logiczna") AND ((Sklep.promocja)="true"));

Robimy to:

SELECT Sum(Sklep.cena)
FROM sklep INNER JOIN Gry ON Sklep.id_gry = Gry.id_gry
WHERE Gry.kategoria="logiczna" AND Sklep.promocja=true;

SELECT Sum(Sklep.cena)

FROM sklep INNER JOIN Gry ON Sklep.id_gry = Gry.id_gry

WHERE Gry.kategoria="logiczna" AND Sklep.promocja=true;

W kluczu jest trochę inna kolejność, jednak nie ma to znaczenia.

Wpisy, które mogą Cię zainteresować:

ROZWIĄZANIA: Matura z informatyki – maj 2023

Zadanie 1 – Biblioteczka Adama

Zadanie 1.1.

Zadanie 1.2.

Zadanie 1.3.

Zadanie 2 – Liczby binarne

Zadanie 2.1.

Zadanie 2.2.

Zadanie 2.3.

Zadanie 2.4.

Zadanie 2.5.

Pełny kod 2.1-2.5 – implementacja w python, C++ i java

Zadanie 3 – Liczba Pi

Zadanie 3.1.

Zadanie 3.2.

Zadanie 3.3.

Zadanie 3.4.

Pełny kod 3.1-3.4 – implementacja w python, C++ i java

Zadanie 4 – Oceń prawdziwość podanych zdań

Zadanie 5 – Systemy pozycyjne

Zadanie 6 – Konfitury owocowe

Zadanie 6.1.

Zadanie 6.2.

Zadanie 6.3.

Zadanie 6.4.

Zadanie 7 – Gry planszowe

Zadanie 7.1.

Zadanie 7.2.

Zadanie 7.3.

Zadanie 7.4.

Zadanie 7.5.

ROZWIĄZANIA Matura z informatyki maj 2021

Terminy matur 2025: harmonogram, czas trwania i wyniki

Matura z informatyki – dlaczego Python jest najlepszym wyborem?

Dbamy o prywatność Twoich danych

Mapa witryny: Korepetycje z informatyki

Polecane wpisy na blogu poświęconemu nauce informatyki